
【题目】如图,∠AOP=∠BOP=15°,PC∥OA,PD⊥OA,若PC=4,则PD的长为 . 
【答案】2
【解析】解:过P作PE⊥OB,交OB与点E,

∵∠AOP=∠BOP,PD⊥OA,PE⊥OB,
∴PD=PE,
∵PC∥OA,
∴∠CPO=∠POD,
又∠AOP=∠BOP=15°,
∴∠CPO=∠BOP=15°,
又∠ECP为△OCP的外角,
∴∠ECP=∠COP+∠CPO=30°,
在直角三角形CEP中,∠ECP=30°,PC=4,
∴PE= ![]() PC=2,
PC=2,
则PD=PE=2.
故答案为:2.
过P作PE垂直与OB,由∠AOP=∠BOP,PD垂直于OA,利用角平分线定理得到PE=PD,由PC与OA平行,根据两直线平行得到一对内错角相等,又OP为角平分线得到一对角相等,等量代换可得∠COP=∠CPO,又∠ECP为三角形COP的外角,利用三角形外角的性质求出∠ECP=30°,在直角三角形ECP中,由30°角所对的直角边等于斜边的一半,由斜边PC的长求出PE的长,即为PD的长.


科目:初中数学 来源: 题型:
【题目】下列因式分解正确的是( )
A.x2﹣2x﹣1=(x﹣1)2
B.2x2﹣2=2(x+1)(x﹣1)
C.x2y﹣xy=y(x2﹣x)
D.x2﹣2x+2=(x﹣1)2+1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列4个命题中:①过直线外一点有且只有一条直线与这条直线平行;②平行于同一条直线的两条直线平行;③两条直线被第三条直线所截,同旁内角互补;④对顶角相等.其中真命题有_____个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题:如图(1),点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,试判断BE、EF、FD之间的数量关系.
【发现证明】小聪把△ABE绕点A逆时针旋转90°至△ADG,从而发现EF=BE+FD,请你利用图(1)证明上述结论.
【类比引申】如图(2),四边形ABCD中,∠BAD≠90°,AB=AD,∠B+∠D=180°,点E、F分别在边BC、CD上,则当∠EAF与∠BAD满足 关系时,仍有EF=BE+FD.
【探究应用】如图(3),在某公园的同一水平面上,四条通道围成四边形ABCD.已知AB=AD=80米,∠B=60°,∠ADC=120°,∠BAD=150°,道路BC、CD上分别有景点E、F,且AE⊥AD,DF=40(![]() ﹣1)米,现要在E、F之间修一条笔直道路,求这条道路EF的长(结果取整数,参考数据:
﹣1)米,现要在E、F之间修一条笔直道路,求这条道路EF的长(结果取整数,参考数据: ![]() =1.41,
=1.41, ![]() =1.73)
=1.73)
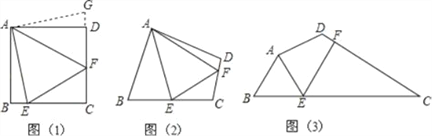
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017·辽宁鞍山一模)甲、乙两人进行慢跑练习,慢跑路程y(单位:m)与所用时间t(单位:min)之间的关系如图所示,下列说法错误的是( )

A. 前2 min,乙的平均速度比甲快
B. 甲、乙两人8 min各跑了800 m
C. 5 min时两人都跑了500 m
D. 甲跑完800 m的平均速度为100 m/min
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y1=kx+2与x轴交于点A(m,0)(m>4),与y轴交于点B,抛物线y2=ax2﹣4ax+c(a<0)经过A,B两点.P为线段AB上一点,过点P作PQ∥y轴交抛物线于点Q.
(1)当m=5时,
①求抛物线的关系式;
②设点P的横坐标为x,用含x的代数式表示PQ的长,并求当x为何值时,PQ=![]() ;
;
(2)若PQ长的最大值为16,试讨论关于x的一元二次方程ax2﹣4ax﹣kx=h的解的个数与h的取值范围的关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=﹣![]() x2+
x2+![]() x+3的图象与x轴交于点A、B,与y轴交于点C,点D在该抛物线上,且点D的横坐标为2,连接BC、BD.设∠OCB=α,∠DBC=β,则cos(α-β)的值是( )
x+3的图象与x轴交于点A、B,与y轴交于点C,点D在该抛物线上,且点D的横坐标为2,连接BC、BD.设∠OCB=α,∠DBC=β,则cos(α-β)的值是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com