

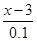 ×10)个粽子,根据题意列方程得:(x-2)(500-
×10)个粽子,根据题意列方程得:(x-2)(500-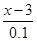 ×10)=800,解得x1=4,x2=6,还应根据实际问题确定两个值是否都满足条件,本题因物价局规定,售价不能超过进价的240%,即2×240%=4.8(元),所以x2=6不合题意,舍去,得x=4;
×10)=800,解得x1=4,x2=6,还应根据实际问题确定两个值是否都满足条件,本题因物价局规定,售价不能超过进价的240%,即2×240%=4.8(元),所以x2=6不合题意,舍去,得x=4;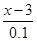 ×10)="800" .
×10)="800" .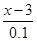 ×10)
×10)

 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:初中数学 来源:不详 题型:填空题
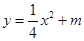 (m<0)与x轴相交于A、B两点(点A在点B的左侧).若点M、N的坐标分别为(0,—2)、(4,0),抛物线与直线MN始终有交点,线段AB的长度的最小值为 .
(m<0)与x轴相交于A、B两点(点A在点B的左侧).若点M、N的坐标分别为(0,—2)、(4,0),抛物线与直线MN始终有交点,线段AB的长度的最小值为 .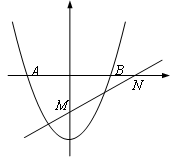
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
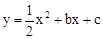 (b,c是常数,且c<0)与x轴分别交于点A,B(点A位于点B的左侧),与y轴的负半轴交于点C,点A的坐标为(-1,0).
(b,c是常数,且c<0)与x轴分别交于点A,B(点A位于点B的左侧),与y轴的负半轴交于点C,点A的坐标为(-1,0).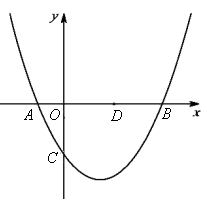
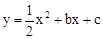 交于点E.点D是x轴上一点,其坐标为
交于点E.点D是x轴上一点,其坐标为查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
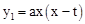 (a为常数,a>0),该抛物线与斜边AB交于点E,直线OA:y2=kx(k为常数,k>0)
(a为常数,a>0),该抛物线与斜边AB交于点E,直线OA:y2=kx(k为常数,k>0)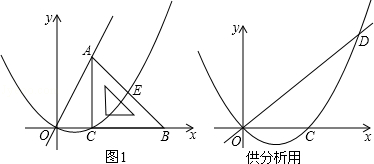
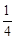 时:
时: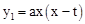 的顶点在函数
的顶点在函数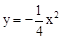 的图象上;
的图象上;查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
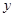 轴对称.
轴对称.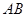 ∥
∥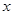 轴,
轴,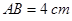 ,最低点
,最低点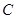 在
在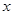 轴上,高
轴上,高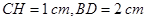 ,则右轮廓线
,则右轮廓线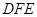 所在抛物线的函数解析式为( )
所在抛物线的函数解析式为( )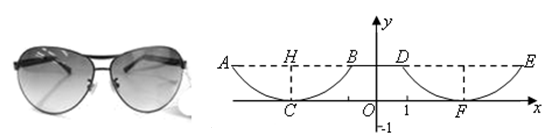
A.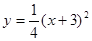 | B.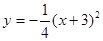 | C.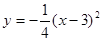 | D.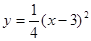 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
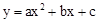 的图象开口向上,对称轴为直线x=1,图象经过(3,0),下列结论中,正确的一项是【 】
的图象开口向上,对称轴为直线x=1,图象经过(3,0),下列结论中,正确的一项是【 】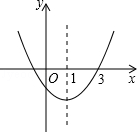
| A.abc<0 | B.2a+b<0 | C.a-b+c<0 | D.4ac-b2<0 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com