
【题目】如图,在△ABC中,AB=AC,D,E分别是边BC,AC上的点,且BD=EC,∠ADE=∠B.
(1)求证:AD=DE;
(2)若∠ADE=![]() ,求∠ADB的度数(用含x的代数式表示).
,求∠ADB的度数(用含x的代数式表示).

【答案】(1)见解析;(2)90°+12x°
【解析】
(1)易证∠B=∠C和∠BAD=∠CDE,即可证明△ABD≌△DCE,根据全等三角形对应边相等性质即可解题;
(2)由(1)结论可得AB=CD,即可求得AC=CD,即可求得∠CDE的大小,即可求得∠BAD的值,根据三角形内角和为180°即可解题.
(1)∵AB=AC,
∴∠B=∠C,
∵∠ADC=∠ADE+∠CDE=∠B+∠BAD,∠ADE=∠B,
∴∠BAD=∠CDE,
在△ABD和△DCE中,
∠BAD=∠CDE,∠B=∠C,BD=CE,
∴△ABD≌△DCE(AAS),
∴AD=DE;
(2)∵△ABD≌△DCE,
∴AB=CD,
∵AB=AC,
∴AC=CD,
∵∠B=∠C=∠ADE=x°,
∴∠CDA=![]() (180°x°),
(180°x°),
∴∠CDE=∠CDA∠ADE=![]() (180°x°)x°=90°
(180°x°)x°=90°![]() x°,
x°,
∴∠BAD=90°![]() x°,
x°,
∴∠ADB=180°∠B∠BAD=180°x°(90°![]() x°)=90°+
x°)=90°+![]() x°.
x°.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,某渔船在海面上朝正东方向匀速航行,在A处观测到灯塔M在北偏东60°方向上,航行半小时后到达B处,此时观测到灯塔M在北偏东30°方向上,那么该船继续航行到达离灯塔距离最近的位置所需时间是( )
A.10分钟
B.15分钟
C.20分钟
D.25分钟
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠A=100°,BI、CI分别平分∠ABC,∠ACB,则∠BIC=________,若BM、CM分别平分∠ABC,∠ACB的外角平分线,则∠M=__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平行四边形ABCD中,BC=4cm , E为AD的中点,F、G分别为BE、CD的中点,则FG=( )cm . 
A.2
B.3
C.4
D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明的父亲在相距2米的两棵树间拴了一根绳子,给他做了简易的秋千,拴绳子的地方距地面高都是2.5米,绳子自然下垂呈抛物线状,身高1米的小明距较近的那棵树0.5米时,头部刚好接触到绳子. 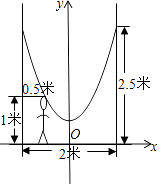
(1)以水平的地面为x轴,两棵树间距离的中点O为原点,建立如图所示的平面直角坐标系,求出抛物线的解析式;
(2)求绳子的最低点离地面的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com