
【题目】已知,如图,在△ABC中,D是BC的中点,DE⊥BC,垂足为D,交AB于点E,且BE2-EA2=AC2,
(1)求证:∠A=90°.
(2)若DE=3,BD=4,求AE的长.

【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)连接CE,由线段垂直平分线的性质可得BE=CE,再结合条件可求得EA2+AC2=CE2,可证得结论;
(2)在Rt△BDE中可求得BE,即求得CE,在Rt△ABC中,利用勾股定理结合已知条件可得到关于AE的方程,可求得AE.
(1)证明
连接CE,如图,
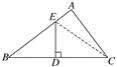
∵D是BC的中点,DE⊥BC,
∴CE=BE
∵BE2-EA2=AC2,
∴CE2-EA2=AC2,
∴EA2+AC2=CE2,
∴△ACE是直角三角形,即∠A=90°;
(2)解 ∵DE=3,BD=4,
∴BE=![]() =5=CE,
=5=CE,
∴AC2=EC2-AE2=25-EA2,
∵BC=2BD=8,
∴在Rt△BAC中,由勾股定理可得:BC2-BA2=64-(5+EA)2=AC2,
∴64-(5+AE)2=25-EA2,解得AE=![]() .
.
故答案为:(1)证明见解析;(2)![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图是一个运算程序:

例如:根据所给的运算程序可知,当![]() 时,
时,![]() ,再把
,再把![]() 代入,得
代入,得![]() ,则输出的结果为
,则输出的结果为![]() .
.
(1)当![]() 时,输出的结果为_________;当
时,输出的结果为_________;当![]() 时,输出结果为_________;
时,输出结果为_________;
(2)若需要经过两次运算才能输出结果,![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了激发学生爱数学、学数学、用数学的热情,某学校在七年级开展“魅力数学”趣味竞赛,该校七年级共有学生400人参加竞赛.现随机抽取40名参赛学生的成绩数据(百分制)进行整理、描述和分析.
74 97 96 89 98 74 69 76 72 78
99 72 97 76 99 74 99 73 98 74
76 88 93 65 78 94 89 68 95 50
89 88 89 89 77 94 87 88 92 91
范围 | 50≤x≤59 | 60≤x≤69 | 70≤x≤79 | 80≤x≤89 | 90≤x≤100 |
频数 | 1 | m | 13 | 9 | 14 |
平均数、中位数、众数如下表所示:
平均数 | 中位数 | 众数 |
84.1 | n | 89 |
根据以上信息,回答下列问题:
(1)m= ,n= ;
(2)小明说:“这次竞赛我得了84分,在所有参赛学生中排名属中等偏上!”小明的说法 (填“正确”或“不正确”),理由是 ;
(3)若成绩不低于85分可以进入决赛,估计参赛的400名学生中能进入决赛的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)2014年益阳市的地区生产总值(第一、二、三产业的增加值之和)已进入千亿元俱乐部,如图表示2014年益阳市第一、二、三产业增加值的部分情况,请根据图中提供的信息解答下列问题

(1)2014年益阳市的地区生产总值为多少亿元?
(2)请将条形统计图中第二产业部分补充完整;
(3)求扇形统计图中第二产业对应的扇形的圆心角度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某网站策划了A、B两种上网的月收费方式:
收费方式 | 月使用费/元 | 包时上网时间/h | 超时费/(元/min) |
A | 30 | 25 | 0.05 |
B | m | n | P |
设每月上网学习时间为x(h)小时,方案A,B的收费金额分别为yA (元)、yB(元).
如图是yB与x之间函数关系的图象
(友情提示:若累计上网时间不超出“包时上网时间”,则只收”月使用费“;若累计上网时间不超出“包时上网时间”,则对超出部分再加收”超时费“)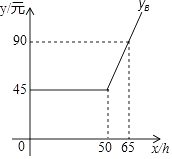
(1)m=;n=p= .
(2)写出yA与x之间的函数关系式.
(3)若每月上网的时间为29小时,请说明选取哪种方式能节省上网费?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=BC,AB=4cm,线段AB上一动点D,以1cm/s的速度从点A出发向终点B运动.过点D作DE⊥AB,交折线AC﹣CB于点E,以DE为一边,在DE左侧作正方形DEFG.设运动时间为x(s)(0<x<4).正方形DEFG与△ABC重叠部分面积为y(cm2).
(1)当x=s时,点F在AC上;
(2)求y关于x的函数解析式,并写出自变量x的取值范围;
(3)设正方形DEFG的中心为点O,直接写出运动过程中,直线BO平分△ABC面积时,自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校举办八年级学生数学素养大赛,比赛共设四个项目:七巧板拼图,趣题巧解,数学应用,魔方复原,每个项目得分都按一定百分比折算后记入总分,下表为甲,乙,丙三位同学得分情况(单位:分)
七巧板拼图 | 趣题巧解 | 数学应用 | 魔方复原 | |
甲 | 66 | 89 | 86 | 68 |
乙 | 66 | 60 | 80 | 68 |
丙 | 66 | 80 | 90 | 68 |
(1)比赛后,甲猜测七巧板拼图,趣题巧解,数学应用,魔方复原这四个项目得分分别按10%,40%,20%,30%折算△记入总分,根据猜测,求出甲的总分;
(2)本次大赛组委会最后决定,总分为80分以上(包含80分)的学生获一等奖,现获悉乙,丙的总分分别是70分,80分.甲的七巧板拼图、魔方复原两项得分折算后的分数和是20分,问甲能否获得这次比赛的一等奖?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知A(0,4)、B(6,0)、C(0,﹣10),平移线段AB至线段CD,点Q在线段DB上,满足S△QOC:S△QOB=5:2,S△QCD=S△QBD,则点Q的坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知线段OA交⊙O于点B,且OB=AB,点P是⊙O上的一个动点,那么∠OAP的最大值是( ) 
A.30°
B.45°
C.60°
D.90°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com