
【题目】小东从甲地出发匀速前往相距20km的乙地,一段时间后,小明从乙地出发沿同一条路匀速前往甲地.小东出发2.5h后,在距乙地7.5km处与小明相遇,之后两人同时到达终点.图中线段AB、CD分别表示小东、小明与乙地的距离y(km)与小东所用时间x(h)的关系.
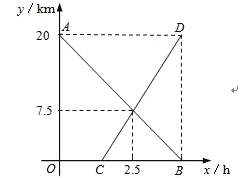
(1)求线段AB、CD所表示的y与x之间的函数表达式;
(2)小东出发多长时间后,两人相距16km?
【答案】(1)线段AB所表示的y与x之间的函数表达式为y1=﹣5x+20;
线段CD所表示的y与x之间的函数表达式为:y2=![]() x﹣
x﹣![]() ;
;
(2)小东出发0.8h或3.7h后,两人相距16km.
【解析】
试题分析:(1)分别利用A,B和(2.5,7.5),D点坐标求出函数解析式得出答案;
(2)利用①当0≤x<1.6时,②当1.6≤x<2.5时,y1﹣y2=16,③当2.5≤x≤4时,分别得出x的值进而得出答案.
试题解析:(1)设线段AB所表示的y与x之间的函数表达式为y1=kx+b,
由图象可知,函数图象经过点(0,20)、(2.5,7.5).
得![]() ,
,
解得:![]() ,
,
所以线段AB所表示的y与x之间的函数表达式为y1=﹣5x+20.
令y1=0,得x=4.
所以B点的坐标为(4,0).所以D点的坐标为(4,20).
设线段CD所表示的y与x之间的函数表达式为y2=mx+n,
因为函数图象经过点(4,20)、(2.5,7.5).
得![]() ,
,
解得: ,
,
所以线段CD所表示的y与x之间的函数表达式为:y2=![]() x﹣
x﹣![]() ;
;
(2)线段CD所表示的y与x之间的函数表达式为y2=![]() x﹣
x﹣![]() ,
,
令y2=0,得x=1.6.即小东出发1.6 h后,小明开始出发.
①当0≤x<1.6时,y1=16,即﹣5x+20=16,
解得:x=0.8,
②当1.6≤x<2.5时,y1﹣y2=16,即﹣5x+20﹣(![]() x﹣
x﹣![]() )=16,
)=16,
解得:x=1.3(舍去)
③当2.5≤x≤4时,y2﹣y1=16,即![]() x﹣
x﹣![]() ﹣(﹣5x+20)=16,
﹣(﹣5x+20)=16,
解得:x=3.7.
答:小东出发0.8h或3.7h后,两人相距16km.


科目:初中数学 来源: 题型:
【题目】适合下列条件的△ABC中,直角三角形的个数为( )
①a=![]() ,b=
,b=![]() ,c=
,c=![]() ②a=6,∠A=45°; ③∠A=32°,∠B=58°;
②a=6,∠A=45°; ③∠A=32°,∠B=58°;
④a=7,b=24,c=25 ⑤a=2,b=2,c=4.
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G、D、C分别在M、N的位置上,若∠EFG=55°,则∠1=______°,∠2=_______°.
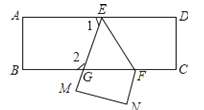
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知a∥b,长方形ABCD的点A在直线a上,B,C,D三点在平面上移动变化(长方形形状大小始终保持不变),请根据如下条件解答:
(1)图1,若点B、D在直线b上,点C在直线b的下方,∠2=30°,则∠1= ;
(2)图2,若点D在直线a的上方,点C在平行直线a,b内,点B在直线b的下方,m,n表示角的度数,请写出m与n的数量关系并说明理由;
(3)图3,若点D在平行直线a,b内,点B,C在直线b的下方,x,y表示角的度数(x>y),且满足关系式x2﹣2xy+y2=100,求x的度数.
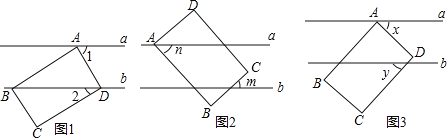
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级共有450名学生,为了了解该年级学生的数学解题能力情况,该校数学兴趣小组随机抽取了90人进行调查分析,并将抽取的学生的数学解题成绩进行分组,绘制如下频数分布表和成绩分布扇形统计图(图1):
该校90名学生数学解题成绩频数分布表

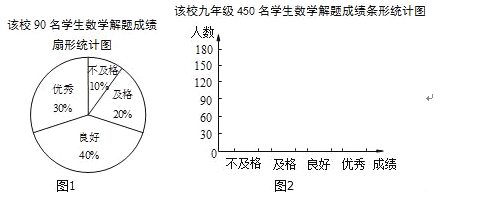
(1)根据抽样调查的结果,将估计出该校九年级450名学生数学解题成绩情况在图2中绘制成条形统计图:
(2)请你结合上述统计的结果,提出一条合理化建议.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com