
【题目】《九章算术》卷九“勾股”中记载:今有池方一丈,葭生其中央,出水一尺.引葭赴岸,适与岸齐.问霞长几何.
注释:今有正方形水池边长1丈,芦苇生长在中央,长出水面1尺.将芦苇向池岸牵引,恰好与水岸齐,问芦苇的长度(一丈等于10尺).解决下列问题:
(1)示意图中,线段![]() 的长为______尺,线段
的长为______尺,线段![]() 的长为______尺;
的长为______尺;

(2)求芦苇的长度.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC是边长为4cm的等边三角形,点P,Q分别从顶点A,B同时出发,沿线段AB,BC运动,且它们的是速度都为1厘米/秒.当点P到达点B时,P、Q两点停止运动.设点P的运动时间为t(秒).
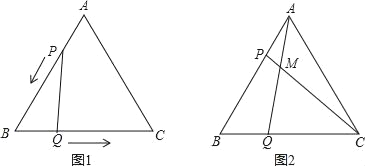
(1)当运动时间为t秒时,AP的长为 厘米,QC的长为 厘米;(用含t的式子表示)
(2)当t为何值时,△PBQ是直角三角形?
(3)连接AQ、CP,相交于点M,如图2,则点P,Q在运动的过程中,∠CMQ会变化吗?若变化,则说明理由;若不变,请求出它的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形OABC中,点A,C分别在x轴,y轴的正半轴上,OA=4,OC=2.点P(m,0)是射线OA上的动点,E为PC中点,作□OEAF,EF交OA于G,
(1)写出点E,F的坐标(用含m的代数式表示):E(_____,_____),F(______,_____).
(2)当线段EF取最小值时,m的值为______;此时□OEAF的周长为______.
(3)①当□OEAF是矩形时,求m的值.
②将△OEF沿EF翻折到△O′EF,若△O′EF与△AEF重叠部分的面积为1时,m的值为 .


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2台大收割机和5台小收割机同时工作2 h共收割小麦3.6hm2,3台大收割机和2台小收割机同时工作5 h共收割小麦8 hm2.1台大收割机和1台小收割机每小时各收割小麦多少公顷?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是
A. “明天降雨的概率是80%”表示明天有80%的时间都在降雨
B. “抛一枚硬币正面朝上的概率为![]() ”表示每抛2次就有一次正面朝上
”表示每抛2次就有一次正面朝上
C. “彩票中奖的概率为1%”表示买100张彩票肯定会中奖
D. “抛一枚正方体骰子,朝上的点数为2的概率为![]() ”表示随着抛掷次数的增加,“抛出朝上的点数为2”这一事件发生的频率稳定在
”表示随着抛掷次数的增加,“抛出朝上的点数为2”这一事件发生的频率稳定在![]() 附近
附近
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校食堂厨房的桌子上整齐地摆放着若干相同规格的碟子,碟子的个数与碟子的高度的关系如下表:
碟子的个数 | 碟子的高度(单位:cm) |
1 | 2 |
2 | 2+1.5 |
3 | 2+3 |
4 | 2+4.5 |
… | … |

(1)当桌子上放有x(个)碟子时,请写出此时碟子的高度(用含x的式子表示);
(2)分别从三个方向上看,其三视图如上图所示,厨房师傅想把它们整齐叠成一摞,求叠成一摞后的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
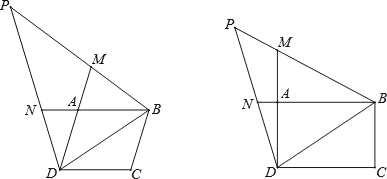
【题目】如图,在平行四边形ABCD中,点M、N分别在线段DA、BA的延长线上,且BD=BN=DM,连接BM、DN并延长交于点P.
(1)求证:∠P=90°﹣![]() ∠C;
∠C;
(2)当∠C=90°,ND=NP时,判断线段MP与AM的数量关系,并给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
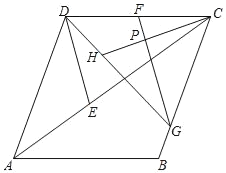
【题目】如图所示,在菱形ABCD中,AC是对角线,CD=CE,连接DE.
(1)若AC=16,CD=10,求DE的长.
(2)G是BC上一点,若GC=GF=CH且CH⊥GF,垂足为P,求证:![]() DH=CF.
DH=CF.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com