
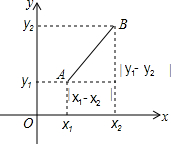
 阅读材料,如图,在平面直角坐标系中,O为坐标原点,对于任意两点A(x1,y1),B(x2,y2).由勾股定理可得:AB2=(x1-x2)2+(y1-y2)2,我们把$\sqrt{({x}_{1}-{x}_{2})^{2}+({y}_{1}-{y}_{2})^{2}}$叫做A,B两点之间的距离,记作AB=$\sqrt{({x}_{1}-{x}_{2})^{2}+({y}_{1}-{y}_{2})^{2}}$
阅读材料,如图,在平面直角坐标系中,O为坐标原点,对于任意两点A(x1,y1),B(x2,y2).由勾股定理可得:AB2=(x1-x2)2+(y1-y2)2,我们把$\sqrt{({x}_{1}-{x}_{2})^{2}+({y}_{1}-{y}_{2})^{2}}$叫做A,B两点之间的距离,记作AB=$\sqrt{({x}_{1}-{x}_{2})^{2}+({y}_{1}-{y}_{2})^{2}}$科目:初中数学 来源: 题型:选择题
| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 总收入/万元 | 总支出/万元 | 结余/万元 | |
| 前年 | x | y | x-y |
| 去年 | 1.2x | 1.15y | 1.2x-1.15y |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
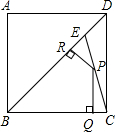 如图:E是边长为1的正方形ABCD的对角线BD上一点,且BE=BC,P为CE上任意一点,PQ⊥BC于点Q,PR⊥BE于点R,则PQ+PR的值是( )
如图:E是边长为1的正方形ABCD的对角线BD上一点,且BE=BC,P为CE上任意一点,PQ⊥BC于点Q,PR⊥BE于点R,则PQ+PR的值是( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com