
【题目】在△ABC中,AB=AC,DE∥BC. 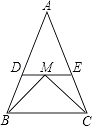
(1)试问△ADE是否是等腰三角形,说明理由;
(2)若M为DE上的点,且BM平分∠ABC,CM平分∠ACB,若△ADE的周长为20,BC=8.求△ABC的周长.
【答案】
(1)解:∵DE∥BC,
∴△ADE∽△ABC.
∴ ![]() =
= ![]() .
.
∵AB=AC,
∴AD=AE.
∴△ADE是等腰三角形
(2)解:∵DE∥BC,BM平分∠ABC,CM平分∠ACB,
∴∠MBC=∠DMB=∠DBM,∠MCB=∠MCE=∠EMC.
∴BD=DM,ME=CE.
∵△ADE的周长=AD+AE+DM+ME=20,
∴AD+AE+BD+CE=20.
∴△ABC的周长=(AD+AE+BD+CE)+BC=20+8=28
【解析】(1)由DE∥BC,可知△ADE∽△ABC,根据相似三角形性质即可求得结论;(2)由于DE∥BC,BM平分∠ABC,CM平分∠ACB,易证BD=DM,ME=CE,根据△ADE的周长为20,BC=8,即可求出△ABC的周长.
【考点精析】通过灵活运用平行线的性质和角平分线的性质定理,掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补;定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上即可以解答此题.


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BC边上的垂直平分线DE与边BC交于点D,边AB交于点E.若△EDC的周长为24,△ABC与四边形AEDC的周长之差为12,则线段DE的长为( ) 
A.12
B.6
C.24
D.36
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是以BC为直径的半圆O的切线,D为半圆上一点,AD=AB,AD,BC的延长线相交于点E.
(1)求证:AD是半圆O的切线;
(2)连结CD,求证:∠A=2∠CDE;
(3)若∠CDE=30°,OB=2,求![]() 的长.
的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是抛物线y=ax2+bx+c(a ≠0)的部分图象,其顶点坐标为(1,n),且与x轴的一个交点在点(3,0)和(4,0)之间.则下列结论:
①a﹣b+c>0; ②3a+b=0; ③b2=4a(c﹣n); ④一元二次方程ax2+bx+c=n﹣1有两个不相等的实数根.
其中正确结论的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】目前节能灯在城市已基本普及,某商场计划购进甲、乙两种节能灯共1200只,这两种节能灯的进价、售价如下表:

(1)如何进货,进货款恰好为46000元?
(2)为确保乙型节能灯顺利畅销,在(1)的条件下,商家决定对乙型节能灯进行打折出售,且全部售完后,乙型节能灯的利润率为20%,请问乙型节能灯需打几折?
查看答案和解析>>
科目:初中数学 来源: 题型:
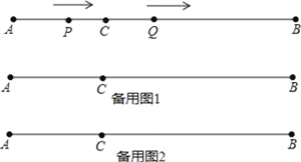
【题目】如图,AB=12cm,点C是线段AB上的一点,BC=2AC.动点P从点A出发,以3cm/s的速度向右运动,到达点B后立即返回,以3cm/s的速度向左运动;动点Q从点C出发,以1cm/s的速度向右运动.设它们同时出发,运动时间为ts.当点P与点Q第二次重合时,P、Q两点停止运动.
(1)AC=__cm,BC=__cm;
(2)当t为何值时,AP=PQ;
(3)当t为何值时,PQ=1cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
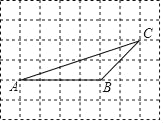
【题目】如图,在方格纸中,点A、B、C是三个格点(网格线的交点叫做格点)
(1)过点C画AB的垂线,垂足为D;
(2)将点D沿BC翻折,得到点E,作直线CE;
(3)直线CE与直线AB的位置关系是 ;
(4)判断:∠ACB ∠ACE.(填“>”、“<”或“=”
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com