
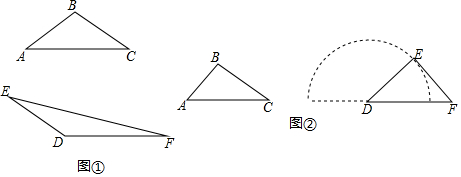
分析 (1)先直接判断出结论,
(2)用三角形的面积公式即可得出结论;
(3)用三角形的面积公式,再用三角函数中正弦值的性质分类讨论即可得出结论.
解答 解:(1)故答案为:C
(2)如图1,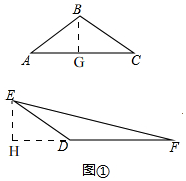
作BG⊥AC垂足为G,作EH⊥DF,垂足为H,
在Rt△BCG中,∠C=30°,
∴BG=BCsin∠C=BCsin30°=$\frac{1}{2}$BC,
∴S1=$\frac{1}{2}$AC×BG=$\frac{1}{2}$AC×$\frac{1}{2}$BC=$\frac{1}{4}$AC×BC
在Rt△EDH中,∠EDH=180°-∠EDF=30°,
∴EH=EDsin∠EDH=EDsin30°=$\frac{1}{2}$ED,
∴S2=$\frac{1}{2}$DF×EH=$\frac{1}{2}$DF×$\frac{1}{2}$ED=$\frac{1}{4}$DF×DE,
∵BC=DE,AC=DF,
∴S1=S2
(3)如图2,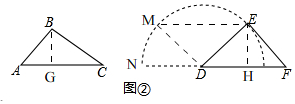 过点B作BG⊥AC,
过点B作BG⊥AC,
①当0°<α≤90°时,
在Rt△BCG中,∠C=30°,
∴BG=BCsin∠C=BCsin30°=$\frac{1}{2}$BC,
∴S1=$\frac{1}{2}$AC×BG=$\frac{1}{2}$AC×$\frac{1}{2}$BC=$\frac{1}{4}$AC×BC,
∵BC=DE,AC=DF,
∴S1=$\frac{1}{4}$DF×DE=$\frac{1}{2}$DF×DE×$\frac{1}{2}$,
在Rt△EDH中,∠EDH=α,
∴EH=EDsin∠EDH=EDsinα,
∴S2=$\frac{1}{2}$DF×EH=$\frac{1}{2}$DF×$\frac{1}{2}$ED=$\frac{1}{2}$DF×DEsinα,
Ⅰ、当sinα<$\frac{1}{2}$时,即:0°<α<30°时,S1>S2,
Ⅱ、当sinα=$\frac{1}{2}$时,即:α=30°时,S1=S2,
Ⅲ、当sinα>$\frac{1}{2}$时,即:30°<α≤90°时,S1<S2,
②当90°<α<180°时,设∠MDN=β=180°-α,
同①方法得,S1=$\frac{1}{2}$DF×DE×$\frac{1}{2}$,
S2=$\frac{1}{2}$DF×DEsinβ,
Ⅰ、当sinβ<$\frac{1}{2}$时,即:0°<β<30°时,
∴0°<180°-α<30°,即:150°<α<180°时,S1>S2,
Ⅱ、当sinβ=$\frac{1}{2}$时,即:β=30°时,即:α=150°时,S1=S2,
Ⅲ、当sinβ>$\frac{1}{2}$时,即:30°<β<90°时,即:90°<α<150°时,S1<S2,
综上所述,
Ⅰ.当α<30°、150°<α<180°时S1>S2;
Ⅱ.当α=30°、α=150°时S1=S2;
Ⅲ.当30°<α<150°时,S1<S2.
点评 此圆的综合题,主要考查了圆的性质,三角形的面积公式,锐角三角函数及其性质,解本题的关键是求出S2,是一道比较简单的综合题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
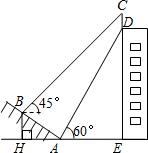 如图,某大楼的顶部有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底部D的仰角为60°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知sin∠BAH=$\frac{1}{2}$,AB=10米,AE=15米.
如图,某大楼的顶部有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底部D的仰角为60°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知sin∠BAH=$\frac{1}{2}$,AB=10米,AE=15米.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①②③⑤ | B. | ①②③ | C. | ①④⑤ | D. | ⑤ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
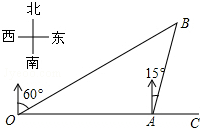 如图,港口A在观测站O的正东方向,OA=4km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为( )
如图,港口A在观测站O的正东方向,OA=4km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为( )| A. | 2$\sqrt{2}$km | B. | 2$\sqrt{3}$km | C. | 4 km | D. | ($\sqrt{3}$+1)km |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com