Question

6．如图，Rt△ABO中，∠AOB=90°，对图形进行下列变换：
①将△ABO沿AO对折，得到△ABD；
②将△ABD绕点O旋转180°，得到△BCD．
（1）画出图形并判断四边形ABCD是什么四边形；
（2）若AO=2$\sqrt{3}$，BO=2，过O作任意一直线交AB于E、交CD于F，则S_BOE+S_△COF=2$\sqrt{3}$（填写最后结果即可，不必写出解答过程）．

Answer 1

分析 （1）先以AO为轴作轴对称变换，再以点O为旋转中心，作出旋转后的图形，由轴对称变换及旋转变换的性质可知该四边形对角线互相平分且垂直，即可知该四边形为菱形；
（2）根据对称性可知△AOE≌△COF，从而可得S_BOE+S_△COF=S_△AOB，即可得答案．

解答 解：（1）如图所示：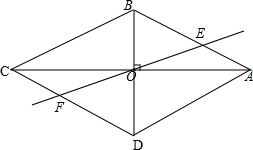

∵△AOD是由△AOB沿AO翻折得到，
∴BO=DO，
∵△BCD是由△ABD绕点O旋转得到，
∴AO=CO，
又∵∠AOB=90°，
∴四边形ABCD是菱形；

（2）∵Rt△ABO中，∠AOB=90°，AO=2$\sqrt{3}$，BO=2
∴S_△AOB=$\frac{1}{2}$•AO•BO=$\frac{1}{2}$×2$\sqrt{3}$×2=2$\sqrt{3}$，
由已知和菱形的对称性可知，△AOE≌△COF
∴S_△BOE+S_△COF=S_△AOB=2$\sqrt{3}$，
故答案为：2$\sqrt{3}$．

点评 本题主要考查轴对称变换、旋转变换及菱形的判定与性质，熟练掌握轴对称变换和旋转变换的性质是解题的关键．