
����Ŀ����ͼ������MΪ���������ABC������һ�㣬����AM��BM��CM����ABΪһ���������ȱ���������ABE����BM�Ƶ�B��ʱ����ת60���õ�BN������EN��
��1����֤����AMB�ա�ENB��
��2����AM+BM+CM��ֵ��С����Ƶ�MΪ��ABC�ķ����㣮����MΪ��ABC�ķ����㣬�����ʱ��AMB����BMC����CMA�Ķ�����
��3��С���������������õ�һ������������η�����ļ�㷽������ͼ�����ֱ�����ABC��AB��ACΪһ���������ȱ���ABE�͵ȱ���ACF������CE��BF���轻��ΪM�����M��Ϊ��ABC�ķ����㣮��˵���������������ݣ�

���𰸡���1������������2����BMC =120�㣻��AMB =120�㣻��AMC=120�㣻��3���߶�EC��BF�Ľ��㼴Ϊ��ABC�ķ����㣮
��������
(1)��ϵȱ������ε����ʣ�����SAS��֤��AMB�ա�ENB��
(2)����MN����(1)�Ľ���֤����BMNΪ�ȱ������Σ�����BM=MN����AM+BM+CM=EN+MN+CM�����Ե�E��N��M��C�ĵ㹲��ʱ��AM+BM+CM��ֵ��С���Ӷ������ʱ��AMB����BMC����CMA�Ķ�����
(3)����(2)�з�����Ķ��壬����ABC�ķ��������߶�EC�ϣ�ͬ��Ҳ���߶�BF�ϣ�����߶�EC��BF�Ľ��㼴Ϊ��ABC�ķ�����.
��1��֤�����ߡ�ABEΪ�ȱ������Σ�
��AB=BE����ABE=60�㣮
����MBN=60�㣬
���ABM=��EBN��
����AMB����ENB��
��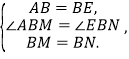
���AMB�ա�ENB��SAS����
��2������MN��
�ɣ�1��֪��AM=EN��
�ߡ�MBN=60�㣬BM=BN��
���BMNΪ�ȱ������Σ�
��BM=MN��
��AM+BM+CM=EN+MN+CM��
����E��N��M��C�ĵ㹲��ʱ��AM+BM+CM��ֵ��С��
��ʱ����BMC=180�㩁��NMB=120�㣻
��AMB=��ENB=180�㩁��BNM=120�㣻
��AMC=360�㩁��BMC����AMB=120�㣮
��3���ɣ�2��֪����ABC�ķ��������߶�EC�ϣ�ͬ��Ҳ���߶�BF�ϣ�
����߶�EC��BF�Ľ��㼴Ϊ��ABC�ķ����㣮
�ʴ�Ϊ����1������������2����BMC =120������AMB =120������AMC=120������3���߶�EC��BF�Ľ��㼴Ϊ��ABC�ķ����㣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��l����A��B���㣬��O���߶�AB�ϵ�һ�㣬��OA=10cm��OB=5cm��
��1������C���߶� AB ���е㣬���߶�CO�ij���
��2�������� P��Q �ֱ�� A��B ͬʱ�����������˶�����P���ٶ�Ϊ4cm/s����Q���ٶ�Ϊ3cm/s�����˶�ʱ��Ϊ x �룬
�ٵ� x=__________��ʱ��PQ=1cm��
������M�ӵ�O��7cm/s���ٶ���P��Q����ͬʱ�����˶����Ƿ���ڳ���m��ʹ��4PM+3OQ��mOMΪ��ֵ�������������mֵ�Լ������ֵ���������ڣ���˵�����ɣ�
��3�������������� OC��OD ��������OAͬʱ�Ƶ�O˳ʱ�뷽����ת��OC��ת���ٶ�Ϊ6��/�룬OD ��ת���ٶ�Ϊ2��/��.��OC��OD��һ���غ�ʱ��OC��OD ͬʱֹͣ��ת������תʱ��Ϊt�룬��tΪ��ֵʱ������ OC��OD��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A��O��B��һ��ֱ���ϣ�OF�ǡ�AOE��ƽ���ߣ�OD�ǡ�BOE��ƽ���ߣ�����DOB=28�㣬���EOF�Ķ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ڣ������̳����д����������һ���Żݹ��│��ע���˿�ֻ��Ϊ�����Ż�ƾ֤���ܶ���������300Ԫ�����ֿ���ƾ����������̳�����۵�8�۹���.
��1���˿������Ԫ������Ʒʱ�����벻��Ǯ��ȣ���ʲô����¹�����㣿
��2��С��Ҫ��һ̨���Ϊ3500Ԫ�ı��䣬��ι�����㣿С���ܽ�ʡ����ԪǮ��
��3��С�Ű�����ķ���������̨�������£�����̳�����ӯ��25������̨����Ľ����Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������֪�߶�AB��20cm����CΪAB�ϵ�һ�����㣬��D��E�ֱ���AC��BC���е�
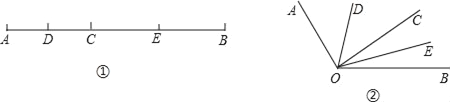
��1������Cǡ����AB�е㣬��DE�ij��Ƕ��٣���ֱ��д�������
��2����BC��14cm����DE�ij�
��3����˵������BCȡ��ֵ��������20cm����DE�ij�����
��4��֪ʶǨ�ƣ���ͼ������֪��AOB��130�㣬���ǵ��ڲ���һ��C������OC����OD��OE�ֱ�ƽ�֡�AOC�͡�BOC���������DOE�Ĵ�С����˵����DOE�Ĵ�С������OC��λ���Ƿ��йأ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����С�������һ�������壬����������ͼ����ͼ��ͼ�������ļ�����ֻ��һ������������Ҫ���ٸ������飿�����Ҫ���ٸ�С�����飿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1����֪3x2-5x+1=0�������и�ʽ��ֵ����3x+![]() ����9x2+
����9x2+![]() ��
��
��2����3xm+1-2xn-1+xn�ǹ���x�Ķ��ζ���ʽ������3��m-n��2-4��n-m��2-��m-n��3+2��n-m��3��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��
���ʱ�����������100m��110m֮�䣬����64m��75m֮�䣬Ϊ��ӭ��2015������ޱ���ij�ؽ�����һ�������ε������䳤�ǿ���1.5���������7560m2�������ж�������������ڹ��ʱ����𣿲�˵��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���з��̽�Ӧ���⣺
Ϊ�������������ļ�ֵ�ۣ�ij������ί��ƻ�����1200����С��ͬ�������������мס���������湫˾���߱�������������ί���ɳ������Ա�ֱ���������湫˾�˽���������������Ϣ��
��Ϣһ����˾������������������������ҹ�˾�������������������������10�죻
��Ϣ�����ҹ�˾ÿ�������������Ǽ�˾ÿ������������1.2����
����������Ϣ����ס���������湫˾ÿ��ֱ����������ٸ���������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com