
【题目】如图,在平面直角坐标系![]() 中,位于第二象限的点
中,位于第二象限的点![]() 在反比例函数
在反比例函数![]() 的图像上,点
的图像上,点![]() 与点
与点![]() 关于原点
关于原点![]() 对称,直线
对称,直线![]() 经过点
经过点![]() ,且与反比例函数
,且与反比例函数![]() 的图像交于点
的图像交于点![]() .
.
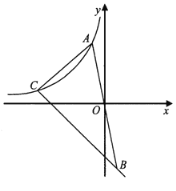
(1)当点![]() 的横坐标是-2,点
的横坐标是-2,点![]() 坐标是
坐标是![]() 时,分别求出
时,分别求出![]() 的函数表达式;
的函数表达式;
(2)若点![]() 的横坐标是点
的横坐标是点![]() 的横坐标的4倍,且
的横坐标的4倍,且![]() 的面积是16,求
的面积是16,求![]() 的值.
的值.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() .
.
【解析】
(1)先将点C坐标代入![]() ,利用待定系数法可求得y1的解析式,继而求得点A的坐标,点B坐标,根据B、C坐标利用待定系数法即可求得y2的解析式;
,利用待定系数法可求得y1的解析式,继而求得点A的坐标,点B坐标,根据B、C坐标利用待定系数法即可求得y2的解析式;
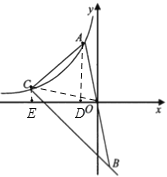
(2)分别过点![]() 作
作![]() 轴于点
轴于点![]() ,
,![]() 轴于点
轴于点![]() ,连接
,连接![]() ,由三角形中线的性质可得
,由三角形中线的性质可得![]() ,再根据反比例函数的比例系数的几何意义可得
,再根据反比例函数的比例系数的几何意义可得![]() ,从而可得
,从而可得![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,则点
,则点![]() 坐标表示为
坐标表示为![]() 、
、![]() ,继而根据梯形的面积公式列式进行计算即可.
,继而根据梯形的面积公式列式进行计算即可.
(1)由已知,点![]() 在
在![]() 的图象上,
的图象上,
∴![]() ,∴
,∴![]() ,
,
∵点![]() 的横坐标为
的横坐标为![]() ,∴点
,∴点![]() 为
为![]() ,
,
∵点![]() 与点
与点![]() 关于原点
关于原点![]() 对称,
对称,
∴![]() 为
为![]() ,
,
把![]()
![]() ,
,![]() 代入
代入![]() 得
得![]() ,
,
解得:![]() ,
,
∴![]() ;
;
(2)分别过点![]() 作
作![]() 轴于点
轴于点![]() ,
,![]() 轴于点
轴于点![]() ,连接
,连接![]() ,
,
∵![]() 为
为![]() 中点 ,
中点 ,
∴![]()
∵点![]() 在双曲线上,
在双曲线上,
∴![]()
∴![]() ,
,
设点![]() 的横坐标为
的横坐标为![]() ,
,
则点![]() 坐标表示为
坐标表示为![]() 、
、![]() ,
,
∴![]() ,
,
解得 ![]() .
.


科目:初中数学 来源: 题型:
【题目】以线段AC为对角线的四边形ABCD(它的四个顶点A,B,C,D按顺时针方向排列),已知AB=BC=CD,∠ABC=100°,∠CAD=40°,则∠BCD的度数为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,点E为BC边上一点,AE和BD交于点F,已知△ABF的面积等于 6,△BEF的面积等于4,则四边形CDFE的面积等于___________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为开展“学生每天锻炼1小时”的活动,我市某中学根据学校实际情况,决定开设A:毽子,B:篮球,C:跑步,D:跳绳四种运动项目.为了了解学生最喜欢哪一种项目,随机抽取了部分学生进行调查,并将调查结果绘制成如图统计图.请结合图中信息解答下列问题:
(1)该校本次调查中,共调查了多少名学生?
(2)计算本次调查学生中喜欢“跑步”的人数和百分比,并请将两个统计图补充完整;
(3)在本次调查的学生中随机抽取1人,他喜欢“跑步”的概率有多大?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,C是⊙O上的一点,连结AC并延长至D,使CD=AC,连结BD,作CE⊥BD,垂足为E。
(1)线段AB与DB的大小关系为 ,请证明你的结论;
(2)判断CE与⊥⊙O的位置关系,并证明;
(3)当△CED与四边形ACEB的面积比是1:7时,试判断△ABD的形状,并证明。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“母亲节”前期,某花店购进康乃馨和玫瑰两种鲜花,销售过程中发现康乃馨比玫瑰销售量大,店主决定将玫瑰每枝降价1元促销,降价后30元可购买玫瑰的数量是原来购买玫瑰数量的1.5倍,求降价后每枝玫瑰的售价是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 为定点,定直线
为定点,定直线![]() ,
,![]() 是直线上一动点,点
是直线上一动点,点![]() 分别为
分别为![]() 的中点,对下列各值: ①线段MN的长;②△PAB的周长;③△PMN的面积;④直线MN,AB之间的距离;⑤∠APB的大小.其中不会随点
的中点,对下列各值: ①线段MN的长;②△PAB的周长;③△PMN的面积;④直线MN,AB之间的距离;⑤∠APB的大小.其中不会随点![]() 的移动而变化的是( )
的移动而变化的是( )

A.②③B.②⑤C.①③④D.④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,丁轩同学在晚上由路灯AC走向路灯BD,当他走到点P时,发现身后他影子的顶部刚好接触到路灯AC的底部,当他向前再步行20m到达Q点时,发现身前他影子的顶部刚好接触到路灯BD的底部,已知丁轩同学的身高是1.5m,两个路灯的高度都是9m,则两路灯之间的距离是( )

A. 24m B. 25m C. 28m D. 30m
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com