
甲、乙两车从 地驶向
地驶向 地,甲车比乙车早行驶
地,甲车比乙车早行驶 ,并且在途中休息了
,并且在途中休息了 ,休息前后速度相同,如图是甲乙两车行驶的距离
,休息前后速度相同,如图是甲乙两车行驶的距离 与时间
与时间 的函数图象,当甲车行驶__________
的函数图象,当甲车行驶__________  时,两车恰好相距
时,两车恰好相距 .
.

科目:初中数学 来源:2017-2018学年苏州市、吴江、相城七年级第一学期期末数学统考试卷 题型:单选题
如图,  ,
,  ,OD平分
,OD平分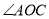 ,则
,则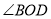 的度数是()
的度数是()

A.  B.
B.  C.
C. 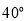 D.
D. 
查看答案和解析>>
科目:初中数学 来源:河北省保定市高阳县2017-2018学年七年级上学期期末考试数学试卷 题型:解答题
解方程
(1)
(2)
查看答案和解析>>
科目:初中数学 来源:河北省保定市高阳县2017-2018学年七年级上学期期末考试数学试卷 题型:单选题
 = ( )
= ( )
A.  B.
B.  C.
C.  D.
D. 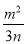
查看答案和解析>>
科目:初中数学 来源:浙江杭州淳安2016-2017学年八年级上学期期末数学试卷 题型:解答题
节约用水是我们的美德,水龙头关闭不严会造成滴水,容器内盛水 与滴水时间
与滴水时间 的关系用可以显示水量的容器做如图
的关系用可以显示水量的容器做如图 的试验,并根据试验数据绘制出如图
的试验,并根据试验数据绘制出如图 的函数图象,结合图象解答下列问题.
的函数图象,结合图象解答下列问题.
( )容器内原有水多少升.
)容器内原有水多少升.
( )求
)求 与
与 之间的函数关系式,并计算在这种滴水状态下一天的滴水量是多少升.
之间的函数关系式,并计算在这种滴水状态下一天的滴水量是多少升.


查看答案和解析>>
科目:初中数学 来源:浙江杭州淳安2016-2017学年八年级上学期期末数学试卷 题型:填空题
函数 中的自变量
中的自变量 的取值范围是__________.
的取值范围是__________.
查看答案和解析>>
科目:初中数学 来源:浙江杭州淳安2016-2017学年八年级上学期期末数学试卷 题型:单选题
在 中和
中和 中,已知
中,已知 ,
,  ,增加下列条件后还不能判定
,增加下列条件后还不能判定 ≌
≌ 的是( ).
的是( ).
A. 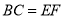 B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源:江苏省2018届九年级上学期期末模拟数学试卷(解析版) 题型:单选题
若a:b=2:3,则下列各式中正确的式子是( )
A. 2a=3b B. 3a=2b C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源:四川省2017-2018学年八年级上学期期末考试数学试卷 题型:解答题
如图,在平面直角坐标系中,直线l1的解析式为y=-x,直线l2与l1交于A点(a,-a)与,与y轴交于点B(0,b),其中a,b满足(a+2)2+ =0 .
=0 .
(1)求直线l2放入解析式;
(2)在平面直角坐标系中第二象限有一点P(m,5),使得S△AOP=S△AOB,请求出点P的坐标;
(3)已知平行于y轴且位于y轴左侧有一动直线,分别与 ,
,  交于点M、N,且点M在点N的下方,点Q为y轴上一动点,且△MNQ为等腰直角三角形,请直接写出满足条件的点Q的坐标.
交于点M、N,且点M在点N的下方,点Q为y轴上一动点,且△MNQ为等腰直角三角形,请直接写出满足条件的点Q的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com