
°ĺŐ‚ńŅ°Ņń≥–£įňńÍľ∂ ż—ß–ň»§–°◊ťĶńÕ¨—ßĶų≤ťŃň»Űł…√Żľ“≥§∂‘°į≥ű÷–…ķīÝ ÷Ľķ…Ō—ß°ĪŌ÷ŌůĶńŅī∑®£¨Õ≥ľ∆’ŻņŪ≤Ę÷∆◊ųŃň»ÁŌ¬ĶńŐű–ő”Ž…»–őÕ≥ľ∆Õľ°£“ņĺ›Õľ÷––ŇŌĘ£¨Ĺ‚īūŌ¬Ń–ő Ő‚£ļ
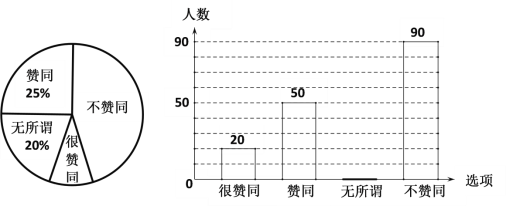
£®1£©Ĺ” ‹’‚īőĶų≤ťĶńľ“≥§Ļ≤”– »ň£Ľ
£®2£©≤Ļ»ęŐű–őÕ≥ľ∆Õľ£Ľ
£®3£©‘ŕ…»–őÕ≥ľ∆Õľ÷–£¨°įļ‹‘řÕ¨°ĪĶńľ“≥§’ľĪĽĶų≤ťľ“≥§◊‹ żĶńįŔ∑÷Ī» « £Ľ
£®4£©‘ŕ…»–őÕ≥ľ∆Õľ÷–,°į≤Ľ‘řÕ¨°ĪĶńľ“≥§≤Ņ∑÷ňý∂‘”¶…»–őĶń‘≤–ńĹ«∂» ż « ∂»£ģ
°ĺīūįł°Ņ£®1£©200£Ľ£®2£©ľŻĹ‚őŲ£Ľ£®3£©10£•£Ľ£®4£©162.
°ĺĹ‚őŲ°Ņ
£ļ(1)”√°į‘řÕ¨°ĪĶńľ“≥§ ż≥ż“‘∂‘”¶ĶńįŔ∑÷Ī»ĺÕ «Ķų≤ťĶńľ“≥§◊‹»ň ż£Ľ
(2)”√Ķų≤ťĶńľ“≥§◊‹»ň ż≥ň°įőřňýőĹ°ĪĶńľ“≥§įŔ∑÷Ī»ĺÕ «°įőřňýőĹ°ĪĶńľ“≥§»ň ż£¨”…īňľīŅ…≤Ļ»ęŐű–őÕ≥ľ∆Õľ£Ľ
(3)”√°įļ‹‘řÕ¨°ĪĶńľ“≥§ ż≥ż“‘◊‹ żľīŅ…Ķ√īūįł£Ľ
(4)”√ °į≤Ľ‘řÕ¨°ĪĶńľ“≥§ňý’ľĶńĪ»ņż≥ň360°„ľīŅ…£ģ
(1)’‚īőĶų≤ťĶńľ“≥§◊‹»ň żő™£ļ50°¬25%=200(»ň)£¨
Ļ īūįłő™£ļ200£Ľ
(2)ĪŪ ĺ°įőřňýőĹ°ĪĶńľ“≥§»ň żő™£ļ200°Ń20%=40(»ň)£¨
≤Ļ»ęŐű–őÕ≥ľ∆Õľ»ÁÕľňý ĺ£ļ

(3)‘ŕ…»–őÕ≥ľ∆Õľ÷–£¨°įļ‹‘řÕ¨°ĪĶńľ“≥§’ľĪĽĶų≤ťľ“≥§◊‹ żĶńįŔ∑÷Ī» «£ļ
![]() °Ń100%=10%£¨
°Ń100%=10%£¨
Ļ īūįłő™£ļ10%£Ľ
(4)°į≤Ľ‘řÕ¨°ĪĶń…»–őĶń‘≤–ńĹ«∂» żő™£ļ![]() °Ń360°„=162°„£¨
°Ń360°„=162°„£¨
Ļ īūįłő™£ļ162.



| ńÍľ∂ | łŖ÷–Ņő≥Ő | ńÍľ∂ | ≥ű÷–Ņő≥Ő |
| łŖ“Ľ | łŖ“Ľ√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű“Ľ | ≥ű“Ľ√‚∑—Ņő≥ŐÕ∆ľŲ£° |
| łŖ∂Ģ | łŖ∂Ģ√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű∂Ģ | ≥ű∂Ģ√‚∑—Ņő≥ŐÕ∆ľŲ£° |
| łŖ»ż | łŖ»ż√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű»ż | ≥ű»ż√‚∑—Ņő≥ŐÕ∆ľŲ£° |
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨ ż÷Š…Ō”– A°ĘB ŃĹĶ„£¨ňýĪŪ ĺĶń”–ņŪ ż∑÷Īūő™ a°Ęb£¨“—÷™ AB=12£¨‘≠Ķ„ O «ŌŖ∂őAB …ŌĶń“ĽĶ„£¨«“ OA=2OB.
![]()
£®1£©«ůa£¨b£Ľ
£®2£©»Ű∂ĮĶ„ P£¨Q ∑÷Īūī” A£¨B Õ¨ Ī≥Ų∑Ę£¨ŌÚ”“‘ň∂Į£¨Ķ„ P ĶńňŔ∂»ő™√Ņ√Ž 2 łŲĶ•őĽ≥§∂»£¨Ķ„ Q ĶńňŔ∂»ő™√Ņ√Ž 1 łŲĶ•őĽ≥§∂»£¨…Ť‘ň∂Į Īľšő™ t √Ž£¨ĶĪĶ„ P ”ŽĶ„ Q ÷ōļŌ Ī£¨P£¨Q ŃĹĶ„Õ£÷Ļ‘ň∂Į.
ĘŔĶĪ t ő™ļő÷Ķ Ī£¨2OPOQ=4£Ľ
ĘŕĶĪĶ„ P ĶĹīÔĶ„ O Ī£¨∂ĮĶ„ M ī”Ķ„ O ≥Ų∑Ę£¨“‘√Ņ√Ž 3 łŲĶ•őĽ≥§∂»ĶńňŔ∂»“≤ŌÚ”“‘ň∂Į£¨ĶĪĶ„ M ◊∑…ŌĶ„ Q ļůŃĘľī∑ĶĽō£¨“‘Õ¨—ýĶńňŔ∂»ŌÚĶ„ P ‘ň∂Į£¨”ŲĶĹĶ„ P ļů‘ŔŃĘľī∑ĶĽō£¨“‘Õ¨—ýĶńňŔ∂»ŌÚĶ„ Q ‘ň∂Į£¨»ÁīňÕý∑Ķ£¨÷ĪĶĹĶ„ P£¨Q Õ£÷Ļ Ī£¨Ķ„ M “≤Õ£÷Ļ‘ň∂Į£¨«ů‘ŕīňĻż≥Ő÷–Ķ„ M –– ĽĶń◊‹¬∑≥Ő£¨≤Ę÷ĪĹ”–ī≥ŲĶ„ M ◊ÓļůőĽ÷√‘ŕ ż÷Š…Ōňý∂‘”¶Ķń”–ņŪ ż.
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
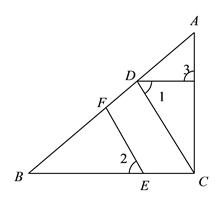
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨°ųABC÷–£¨AB=AC£¨“‘ABő™÷Īĺ∂◊ų°—O£¨ĹĽBC”ŕĶ„D£¨ĹĽCAĶń—”≥§ŌŖ”ŕĶ„E£¨Ń¨Ĺ”AD°ĘDE£ģ 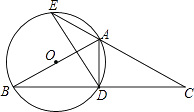
£®1£©«ů÷§£ļD «BCĶń÷–Ķ„£Ľ
£®2£©»ŰDE=3£¨BD©ĀAD=2£¨«ů°—OĶńįŽĺ∂£Ľ
£®3£©‘ŕ£®2£©ĶńŐűľĢŌ¬£¨«ůŌ“AEĶń≥§£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»ÁÕľĘŔ£¨‘ŕ°ųABC÷–£¨°ŌABC”Ž°ŌACBĶń∆Ĺ∑÷ŌŖŌŗĹĽ”ŕĶ„P£ģ
£®1£©»ÁĻŻ°ŌA=80°„£¨«ů°ŌBPCĶń∂» ż£Ľ
£®2£©»ÁÕľĘŕ£¨◊ų°ųABCÕ‚Ĺ«°ŌMBC£¨°ŌNCBĶńĹ«∆Ĺ∑÷ŌŖĹĽ”ŕĶ„Q£¨ ‘ŐĹňų°ŌQ°Ę°ŌA÷ģľšĶń żŃŅĻōŌĶ£ģ
£®3£©»ÁÕľĘŘ£¨—”≥§ŌŖ∂őBP°ĘQCĹĽ”ŕĶ„E£¨°ųBQE÷–£¨īś‘ŕ“ĽłŲńŕĹ«Ķ»”ŕŃŪ“ĽłŲńŕĹ«Ķń2Ī∂£¨«ů°ŌAĶń∂» ż.


≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°ŅŌ¬Ń–ňĶ∑®’ż»∑Ķń «( )
A. ≥§∑Ĺ–őĶń≥§ «![]() √◊,ŅŪĪ»≥§∂Ő25√◊,‘ÚňŁĶń÷‹≥§Ņ…ĪŪ ĺő™
√◊,ŅŪĪ»≥§∂Ő25√◊,‘ÚňŁĶń÷‹≥§Ņ…ĪŪ ĺő™![]() √◊
√◊
B. ![]() ĪŪ ĺĶ◊ő™6,łŖő™
ĪŪ ĺĶ◊ő™6,łŖő™![]() Ķń»żĹ«–őĶń√śĽż
Ķń»żĹ«–őĶń√śĽż
C. ![]() ĪŪ ĺ“ĽłŲŃĹőĽ ż,ňŁĶńłŲőĽ ż◊÷ «
ĪŪ ĺ“ĽłŲŃĹőĽ ż,ňŁĶńłŲőĽ ż◊÷ «![]() ģőĽ ż◊÷ «
ģőĽ ż◊÷ «![]()
D. ľ◊°Ę““ŃĹ»ň∑÷Īūī”Ōŗĺŗ40«ß√◊ĶńŃĹĶōŌŗŌÚ≥Ų∑Ę,∆š––◊ŖĶńňŔ∂»∑÷Īūő™3«ß√◊/–° ĪļÕ5«ß√◊/–° Ī,ĺ≠Ļż![]() –° ĪŌŗ”Ų,‘ÚŅ…Ń–∑Ĺ≥Őő™
–° ĪŌŗ”Ų,‘ÚŅ…Ń–∑Ĺ≥Őő™![]()
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨‘ŕRt°ųABC÷–£¨°ŌACB=90°„£¨AC=4£¨BC=6£¨Ķ„D «ĪŖBCĶń÷–Ķ„£¨Ķ„E «ĪŖAB…ŌĶń»ő“‚“ĽĶ„£®Ķ„E≤Ľ”ŽĶ„B÷ōļŌ£©£¨—ōDE∑≠’Ř°ųDBE ĻĶ„B¬š‘ŕĶ„Fī¶£¨Ń¨Ĺ”AF£¨‘ÚŌŖ∂őAFĶń≥§»°◊Ó–°÷Ķ Ī£¨BFĶń≥§ő™ £ģ 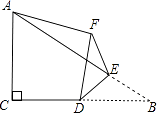
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨‘ŕňńĪŖ–őABCD÷–£¨°ŌA+°ŌD=¶Ń£¨°ŌABCĶń∆Ĺ∑÷ŌŖ”Ž°ŌBCDĶń∆Ĺ∑÷ŌŖĹĽ”ŕĶ„P£¨‘Ú°ŌPĶ»”ŕ________∂»£®”√ļ¨”–¶ŃĶń Ĺ◊”ĪŪ ĺ£©

≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ“—÷™ňńĪŖ–őABCD «∆Ĺ––ňńĪŖ–ő£®»ÁÕľ£©£¨į—°ųABD—ō∂‘Ĺ«ŌŖBD∑≠’Ř180°„Ķ√ĶĹ°ųA®@BD.
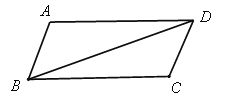
£®1£©ņŻ”√≥ŖĻś◊ų≥Ų°ųA®@BD.£®“™«ůĪ£ŃŰ◊ųÕľļŘľ££¨≤Ľ–ī◊ų∑®£©£Ľ
£®2£©…ŤD A®@ ”ŽBCĹĽ”ŕĶ„E£¨«ů÷§£ļ°ųBA®@E°’°ųDCE.
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨‘ŕ![]() ÷–£¨
÷–£¨ ![]() £¨īĻ◊„ő™
£¨īĻ◊„ő™![]() £¨Ķ„
£¨Ķ„![]() ‘ŕ
‘ŕ![]() …Ō£¨
…Ō£¨ ![]() £¨īĻ◊„ő™
£¨īĻ◊„ő™![]() .
.
£®1£©![]() ”Ž
”Ž![]() ∆Ĺ––¬ū£Ņő™ ≤√ī£Ņ
∆Ĺ––¬ū£Ņő™ ≤√ī£Ņ
£®2£©»ÁĻŻ![]() £¨«“
£¨«“![]() £¨«ů
£¨«ů![]() Ķń∂» ż.
Ķń∂» ż.
≤ťŅīīūįłļÕĹ‚őŲ>>
įŔ∂»÷¬–Ň - Ń∑Ōį≤ŠŃ–ĪŪ - ‘Ő‚Ń–ĪŪ
ļĢĪĪ °Ľ•Ń™ÕÝő•∑®ļÕ≤ĽŃľ–ŇŌĘĺŔĪ®∆ĹŐ® | ÕÝ…Ō”–ļ¶–ŇŌĘĺŔĪ®◊®«Ý | ĶÁ–Ň’©∆≠ĺŔĪ®◊®«Ý | …śņķ ∑–ťőř÷ų“Ś”–ļ¶–ŇŌĘĺŔĪ®◊®«Ý | …ś∆ů«÷»®ĺŔĪ®◊®«Ý
ő•∑®ļÕ≤ĽŃľ–ŇŌĘĺŔĪ®ĶÁĽį£ļ027-86699610 ĺŔĪ®” Ōš£ļ58377363@163.com