
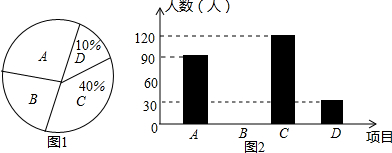
���� ��1����C��������������ռ�İٷֱȼ��ɵõ��������������
��2���ȷֱ�����B��������A��B������ռ�İٷֱȣ�Ȼ��ȫͳ��ͼ��
��3�����������������壬��������B�������İٷֱ���ΪȫУϲ�������֡��������İٷֱȣ�Ȼ���ô˰ٷֱȳ���ȫУ�������ɵõ�ȫУϲ�������֡���������
��4���Ȼ���״ͼչʾ����12�ֵȿ��ܵĽ���������ҳ���ͬ�Ա��ѧ���Ľ������Ȼ����ݸ��ʹ�ʽ��⣮
��� �⣺��1��120��40%=300��������
��������ε����У���������300��ѧ����
��2��B��ѧ������=300-90-120-30=60��������
A��������ռ�ٷֱ�=$\frac{90}{300}$��100%=30%��B��������ռ�ٷֱ�=$\frac{60}{300}$��100%=20%��
ͳ��ͼΪ��
��3��2000��20%=400���ˣ���
���Թ���ϲ�������֡�������ԼΪ400�ˣ�
��4������״ͼΪ��
����12�ֵȿ��ܵĽ������������ͬ�Ա��ѧ���Ľ����Ϊ4��
������ͬ�Ա��ѧ���ĸ���=$\frac{4}{12}$=$\frac{1}{3}$��
���� ���⿼�����б�������״ͼ���������б�������״ͼ��չʾ���п��ܵĽ�����n���ٴ���ѡ�������¼�A��B�Ľ����Ŀm��������ʣ�Ҳ������ͳ��ͼ���������������壮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 10 | B�� | 11 | C�� | 12 | D�� | 13 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
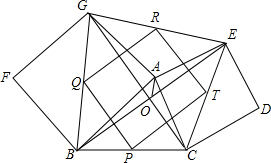 ��ͼ����֪��ABC���ֱ���AB��ACΪ����������ABFG��������ACDE������BE��CG���ڵ�O������AO��P��Q��R��T�ֱ���BC��BG��EG��CE���е㣮
��ͼ����֪��ABC���ֱ���AB��ACΪ����������ABFG��������ACDE������BE��CG���ڵ�O������AO��P��Q��R��T�ֱ���BC��BG��EG��CE���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ABC�У�AB=AC��DΪ��ABC��һ�㣬�ҡ�BDC=��BAC��BD��AC��O��AM��BD��M
��ͼ����ABC�У�AB=AC��DΪ��ABC��һ�㣬�ҡ�BDC=��BAC��BD��AC��O��AM��BD��M �鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
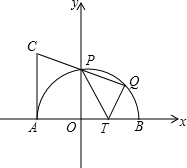 ��ͼ����ƽ��ֱ������ϵ�У��뾶Ϊ2�İ�ԲO��x�ύ��A��B���㣬��y�ύ�ڵ�P��T��OB�ϵ�һ�㣬OT=a��0��a��2������A��AC��AB����AC=AT������CP���ӳ�����Բ����һ��Q����QǡΪ��PB�е㣮
��ͼ����ƽ��ֱ������ϵ�У��뾶Ϊ2�İ�ԲO��x�ύ��A��B���㣬��y�ύ�ڵ�P��T��OB�ϵ�һ�㣬OT=a��0��a��2������A��AC��AB����AC=AT������CP���ӳ�����Բ����һ��Q����QǡΪ��PB�е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
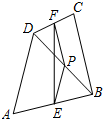 ��ͼ�����ı���ABCD�У�P�ǶԽ���BD���е㣬E��F�ֱ���AB��CD���е㣬AD=BC����PEF=10�㣬���PFE�Ķ�����10�㣮
��ͼ�����ı���ABCD�У�P�ǶԽ���BD���е㣬E��F�ֱ���AB��CD���е㣬AD=BC����PEF=10�㣬���PFE�Ķ�����10�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com