
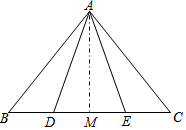
 已知点D、E在△ABC的BC边上,AD=AE,BD=CE,为了判断∠B与∠C的大小关系,请你填空完成下面的推理过程,并在空白括号内,注明推理的根据.
已知点D、E在△ABC的BC边上,AD=AE,BD=CE,为了判断∠B与∠C的大小关系,请你填空完成下面的推理过程,并在空白括号内,注明推理的根据. 分析 首先根据等腰三角形的性质,得DM=EM,结合已知条件,根据等式的性质,得BM=CM,从而根据线段垂直平分线的性质,得AB=AC,再根据等腰三角形的性质即可证明.
解答  解:作AM⊥BC,垂足为M
解:作AM⊥BC,垂足为M
∵AD=AE,
∴△ADE是等腰三角形,
∴DM=EM (等腰三角形底边上的高也是底边上的中线)
又∵BD=CE,
∴BD+DM=CE+EM,即BM=CM;
又∵AM⊥BC(自己所作),
∴AM是线段BC的垂直平分线;
∴AB=AC (线段垂直平分线上的点到线段两个端点的距离相等)
∴∠B=∠C.
故答案为:等腰,等腰三角形底边上的高也是底边上的中线,CE+EM,CM,AM⊥BC,BC,线段垂直平分线上的点到线段两个端点的距离相等,∠B=∠C.
点评 此题综合考查了等腰三角形的性质、线段垂直平分线的性质.等腰三角形底边上的高、底边上的中线、顶角的平分线互相重合;等腰三角形的两个底角相等.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com