
 如图,在△ABC的角平分线CD,BE相交于F,∠A=90°,EG∥BC,且EG⊥CG于G,下列说法:
如图,在△ABC的角平分线CD,BE相交于F,∠A=90°,EG∥BC,且EG⊥CG于G,下列说法:| A. | 只有①③ | B. | 只有②④ | C. | 只有①③④ | D. | ①②③④ |
分析 根据平行线、角平分线、垂直的性质及三角形内角和定理依次判断即可得出答案.
解答 解:①∵EG∥BC,
∴∠CEG=∠ACB,
又∵CD是△ABC的角平分线,
∴∠CEG=∠ACB=2∠DCB,故①正确;
②无法证明CA平分∠BCG,故②错误;
③∵∠A=90°,
∴∠ADC+∠ACD=90°,
∵CD平分∠ACB,
∴∠ACD=∠BCD,
∴∠ADC+∠BCD=90°.
∵EG∥BC,且CG⊥EG,
∴∠GCB=90°,即∠GCD+∠BCD=90°,
∴∠ADC=∠GCD,故③正确;
④∵∠EBC+∠ACB=∠AEB,∠DCB+∠ABC=∠ADC,
∴∠AEB+∠ADC=90°+$\frac{1}{2}$(∠ABC+∠ACB)=135°,
∴∠DFE=360°-135°-90°=135°,
∴∠DFB=45°=$\frac{1}{2}$∠CGE,故④正确.
故选C.
点评 本题考查的是三角形内角和定理,熟知直角三角形的两锐角互余是解答此题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
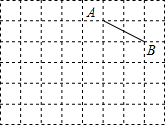 如图,在每个小正方形的边长均为1的方格纸中,有线段AB,点A、B均在小正方形的顶点上.
如图,在每个小正方形的边长均为1的方格纸中,有线段AB,点A、B均在小正方形的顶点上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
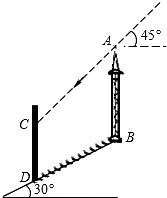 如图,在坡角为30°的山坡上有一铁塔AB,其正前方 矗立着一大型广告牌,当阳光与水平线成45°角时,测得铁塔AB落在斜坡上的影子BD的长为4米,落在广告牌上的影子CD的长为3米,求铁塔AB的高(AB,CD均与水平面垂直,结果保留根号).
如图,在坡角为30°的山坡上有一铁塔AB,其正前方 矗立着一大型广告牌,当阳光与水平线成45°角时,测得铁塔AB落在斜坡上的影子BD的长为4米,落在广告牌上的影子CD的长为3米,求铁塔AB的高(AB,CD均与水平面垂直,结果保留根号).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com