
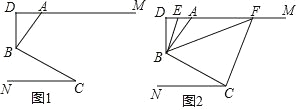
【题目】已知如图1,在△ABC中,∠ACB=90°,BC=AC,点D在AB上,DE⊥AB交BC于E,点F是AE的中点
(1)写出线段FD与线段FC的关系并证明;
(2)如图2,将△BDE绕点B逆时针旋转α(0°<α<90°),其它条件不变,线段FD与线段FC的关系是否变化,写出你的结论并证明;
(3)将△BDE绕点B逆时针旋转一周,如果BC=4,BE=2![]() ,直接写出线段BF的范围.
,直接写出线段BF的范围.

【答案】(1)结论:FD=FC,DF⊥CF.理由见解析;(2)结论不变.理由见解析;(3)![]() ≤BF
≤BF![]() .
.
【解析】
(1)结论:FD=FC,DF⊥CF.由直角三角形斜边中线定理即可证明;
(2)如图2中,延长AC到M使得CM=CA,延长ED到N,使得DN=DE,连接BN、BM.EM、AN,延长ME交AN于H,交AB于O.想办法证明△ABN≌△MBE,推出AN=EM,再利用三角形中位线定理即可解决问题;
(3)分别求出BF的最大值、最小值即可解决问题;
解:(1)结论:FD=FC,DF⊥CF.
理由:如图1中,
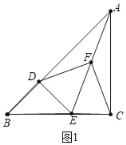
∵∠ADE=∠ACE=90°,AF=FE,
∴DF=AF=EF=CF,
∴∠FAD=∠FDA,∠FAC=∠FCA,
∴∠DFE=∠FDA+∠FAD=2∠FAD,∠EFC=∠FAC+∠FCA=2∠FAC,
∵CA=CB,∠ACB=90°,
∴∠BAC=45°,
∴∠DFC=∠EFD+∠EFC=2(∠FAD+∠FAC)=90°,
∴DF=FC,DF⊥FC.
(2)结论不变.
理由:如图2中,延长AC到M使得CM=CA,延长ED到N,使得DN=DE,连接BN、BM.EM、AN,延长ME交AN于H,交AB于O.
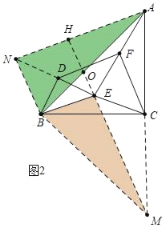
∵BC⊥AM,AC=CM,
∴BA=BM,同法BE=BN,
∵∠ABM=∠EBN=90°,
∴∠NBA=∠EBM,
∴△ABN≌△MBE,
∴AN=EM,∴∠BAN=∠BME,
∵AF=FE,AC=CM,
∴CF=![]() EM,FC∥EM,同法FD=
EM,FC∥EM,同法FD=![]() AN,FD∥AN,
AN,FD∥AN,
∴FD=FC,
∵∠BME+∠BOM=90°,∠BOM=∠AOH,
∴∠BAN+∠AOH=90°,
∴∠AHO=90°,
∴AN⊥MH,FD⊥FC.
(3)![]() .
.
当点![]() 落在
落在![]() 上时,
上时,![]() 取得最大值,
取得最大值,
如图5所示,∵![]() ,
,![]() ,
,![]() ,∴
,∴![]() ,
,
∵![]() 是
是![]() 的中点,∴
的中点,∴![]() ,
,
又![]() ,
,
∴![]() ,
,
即![]() 的最大值为
的最大值为![]() .
.
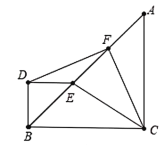
图5
当点![]() 落在
落在![]() 延长线上时,
延长线上时,![]() 取得长最小值,
取得长最小值,
如图6所示,∵![]() ,
,![]() ,
,![]() ,∴
,∴![]() ,
,
∵![]() 是
是![]() 的中点,∴
的中点,∴![]() ,
,
又![]() ,
,
∴![]() ,
,
即![]() 的最小值为
的最小值为![]() .
.
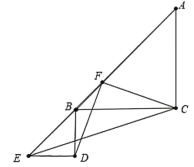
图6
综上所述,![]() .
.


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=36°,∠C=72°,点D在AC上,BC=BD,DE∥BC交AB于点E,则图中等腰三角形共有( )

A. 3个B. 4个C. 5个D. 6个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC和△DCE中,CA=CB,CD=CE,∠CAB= ∠CED=α.
(1)如图1,将AD、EB延长,延长线相交于点0.
①求证:BE= AD;
②用含α的式子表示∠AOB的度数(直接写出结果);
(2)如图2,当α=45°时,连接BD、AE,作CM⊥AE于M点,延长MC与BD交于点N.求证:N是BD的中点.
注:第(2)问的解答过程无需注明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=-2x与直线y=kx+b相交于点A(a,2),并且直线y=kx+b经过x轴上点B(2,0).
(1)求直线y=kx+b的解析式;
(2)求两条直线与y轴围成的三角形面积;
(3)直接写出不等式(k+2)x+b≥0的解集.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明参加某网店的“翻牌抽奖”活动.如图,4张牌分别对应价值5,10,15,20(单位:元)的4件奖品.

(1)如果随机翻1张牌,求抽中20元奖品的概率;
(2)如果随机翻两张牌,且第一次翻过的牌不再参加下次翻牌,求所获奖品总值不低于30元的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图 1,AM∥CN,点 B 为平面内一点,AB⊥BC 于 B,过 B 作 BD⊥ AM.
(1)求证:∠ABD=∠C;
(2)如图 2,在(1)问的条件下,分别作∠ABD、∠DBC 的平分线交 DM 于 E、F,若∠BFC=1.5∠ABF,∠FCB=2.5∠BCN,
①求证:∠ABF=∠AFB;
②求∠CBE 的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中华文化十大精深,源远流长,我国古代数学著作《增删算法统宗》记载“绳索量竿”问题:“一条竿子一条索,索比竿子短一托。”其大意 为:现有一根竿和一要绳索,折回索子来量竿,却比竿尺;如果将绳索对半折后再去量竿和一条绳索,用绳索去量竿,绳索比竿长5尺;如果绳索对半折后再去量竿,就比竿短5尺.设绳索长![]() 尺,竿长
尺,竿长![]() 尺,则符合题意的方程组是( )
尺,则符合题意的方程组是( )
A. 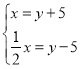 B.
B. 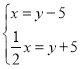 C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com