
分析 (1)根据对称轴,可得h的值,根据抛物线与y轴的交点,可得a值.
(2)根据顶点式,即可说明需要移动的单位和方向.
(3)根据函数图象及函数的增减性回答即可.
解答 解:(1)已知抛物线y=a(x-h)2的对称轴为直线x=-2,
h=-2,
抛物线y=a(x+2)2过点(1,-3),
把(1,-3)代入y=a(x+2)2得
9a=-3,
解得 a=-$\frac{1}{3}$,
所以该抛物线的解析式为y=-$\frac{1}{3}$(x+2)2.
(2)该抛物线是由y=-$\frac{1}{3}$x2经过向左平移2个单位得到;
(3)∵a=-$\frac{1}{3}$,
∴开口向下,在对称轴的右侧,y随x的增大而减小,
∴当x>-2时,y随x的增大而减小;
∵抛物线的顶点为(-2,0),
∴当x=-2时,函数有最大值0.
点评 本题考查了用待定系数法求函数表达式以及二次函数的性质,同时还考查了抛物线的平移等知识,是比较常见的题目.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 数学课上,老师按下面的方法作线段AB的黄金分割点C(如图),
数学课上,老师按下面的方法作线段AB的黄金分割点C(如图),查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增减 | +5 | -2 | 4 | +13 | 10 | +16 | 9 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
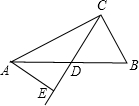 如图,在Rt△ABC中,∠ACB=90°,D为斜边AB的中点,过点A作CD的垂线交CD延长线于点E,AE=3,CE=6,则CD的长为$\frac{15}{4}$.
如图,在Rt△ABC中,∠ACB=90°,D为斜边AB的中点,过点A作CD的垂线交CD延长线于点E,AE=3,CE=6,则CD的长为$\frac{15}{4}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com