
【题目】在升旗结束后,小铭想利用所学数学知识测量学校旗杆高度,如图,旗杆的顶端垂下一绳子,将绳子拉直钉在地上,末端恰好至C处且与地面成60°角,小铭从绳子末端C处拿起绳子后退至E点,求旗杆AB的高度和小铭后退的距离.(单位:米,参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73,结果保留一位小数)
≈1.73,结果保留一位小数)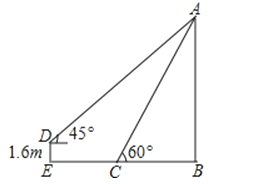
【答案】解:设绳子AC的长为x米;
在△ABC中,AB=ACsin60°,
过D作DF⊥AB于F,如图所示:
∵∠ADF=45°,
∴△ADF是等腰直角三角形,
∴AF=DF=xsin45°,
∵AB﹣AF=BF=1.6,
则xsin60°﹣xsin45°=1.6,
解得:x=10,
∴AB=10×sin60°≈8.7(m),EC=EB﹣CB=xcos45°﹣x×cos60°=10×![]() ﹣10×
﹣10×![]() ≈2.1(m);
≈2.1(m);
答:旗杆AB的高度为8.7m,小铭后退的距离为2.1m.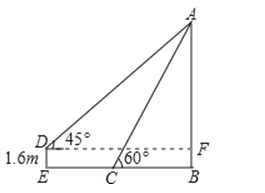
【解析】设绳子AC的长为x米;由三角函数得出AB=ACsin60°,过D作DF⊥AB于F,则△ADF是等腰直角三角形,得出AF=DF=xsin45°,由AB﹣AF=BF=1.6得出方程,解方程求出x,得出AB,再由三角函数即可得出小铭后退的距离.
【考点精析】关于本题考查的解直角三角形,需要了解解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法)才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】没有水就没有生命.地球上的总储量中97%是咸水,余下的是淡水,其中可直接饮用的只有0.5%,大约有105万亿吨,约占淡水总量的![]() , 其余淡水资源集中在两极冰川中,难以利用.目前,世界上近20%的人缺少饮用水,我国的形势也十分严峻,人均可用淡水量比世界人均可用淡水量少25%.
, 其余淡水资源集中在两极冰川中,难以利用.目前,世界上近20%的人缺少饮用水,我国的形势也十分严峻,人均可用淡水量比世界人均可用淡水量少25%.
(1)世界上可用淡水量占淡水总量的百分之几;
(2)世界上只有百分之几的人口不缺饮用水;
(3)我国人均可用淡水量相当于世界人均可用淡水量的百分之几;
(4)世界上的水资源总储量大约为多少万亿吨.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠1和∠2互补,∠C=∠EDF.
(1)判断DF与EC的关系为 .
(2)试判断DE与BC的关系,并说明理由.
(3)试判断∠DEC与∠DFC的关系并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
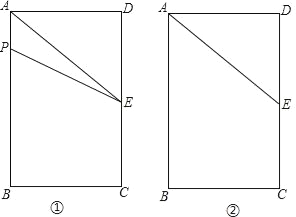
【题目】如图①,长方形ABCD中,AB=6cm,BC=4cm,E为CD的中点.点P从A点出发,沿A﹣B﹣C的方向在长方形边上匀速运动,速度为1cm/s,运动到C点停止.设点P运动的时间为ts.(图②为备用图)
(1)当P在AB上,t= s时,△APE的面积为长方形面积的![]() ;
;
(2)整个运动过程中,t为何值时,△APE为直角三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
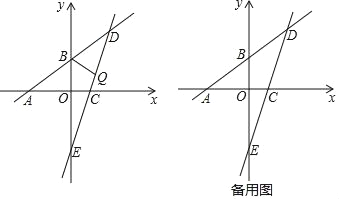
【题目】已知:如图,一次函数![]() 的图象分别与x轴、y轴相交于点A、B,且与经过点C(2,0)的一次函数y=kx+b的图象相交于点D,点D的横坐标为4,直线CD与y轴相交于点E.
的图象分别与x轴、y轴相交于点A、B,且与经过点C(2,0)的一次函数y=kx+b的图象相交于点D,点D的横坐标为4,直线CD与y轴相交于点E.
(1)直线CD的函数表达式为 ;(直接写出结果)
(2)点Q为线段DE上的一个动点,连接BQ.
①若直线BQ将△BDE的面积分为1:2两部分,试求点Q的坐标;
②将△BQD沿着直线BQ翻折,使得点D恰好落在直线AB下方的坐标轴上,请直接写出点Q的坐标: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,湖中的小岛上有一标志性建筑物,其底部为A,某人在岸边的B处测得A在B的北偏东30°的方向上,然后沿岸边直行4公里到达C处,再次测得A在C的北偏西45°的方向上(其中A、B、C在同一平面上).求这个标志性建筑物底部A到岸边BC的最短距离.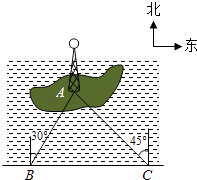
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题:①对顶角相等;②同位角相等,两直线平行;③若|a|=|b|,则a=b;④若x=2,则2|x|-1=3.以上命题是真命题的有( ).
A. ①②③④ B. ①④ C. ②④ D. ①②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com