
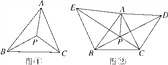
����Ŀ����ͼ����PΪ��ABC����ƽ����һ�㣬�ҡ�APB����BPC����CPA��120�������P������ABC�ķ����㣮
(1)�����PΪ��ǡ�ABC�ķ����㣬�ҡ�ABC��60��.
����֤�� ��ABP�ס�BCP��
����PA��3��PC��4����PB�ij���
(2)��ͼ�ڣ���֪��ǡ�ABC���ֱ���AB��ACΪ������������ABE������ACD��CE��BD�ཻ�ڵ�P������AP.
�����CPD�Ķ�����
����֤����PΪ��ABC�ķ����㣮
���𰸡���1�������� ��2��60�� ��3��������
(1)��֤�����ߡ�PAB����PBA��180������APB��60������PBC����PBA����ABC��60�������PAB����PBC.�֡ߡ�APB����BPC��120�������ABP�ס�BCP
�ڽ⣺�ɢٿ�֪��ABP�ס�BCP���� ![]() ����PB2��PA��PC��12����PB��2
����PB2��PA��PC��12����PB��2![]() .
.
(2)�ٽ⣺��ͼ���ߡ�ABE�͡�ACD���������Σ���AE��AB��AC��AD����EAB����5��60��.�ߡ�EAC����EAB����BAC����BAD����BAC����5�����EAC����BAD�����ACE�ա�ADB�����1����2.�ߡ�3����4�����CPD����5��60��.
��֤�����ɢٿ�֪��1����2����3����4�����ADF�ס�PCF����AF��PF��DF��CF����AF��DF��PF��CF.�ߡ�AFP����CFD�����AFP�ס�DFC�����APF����ACD��60��.�ɢٿ�֪��CPD��60�������APC����CPD����APF��120������BPC��180������CPD��120�������APB��360������BPC����APC��120�������PΪ��ABC�ķ����㣮

����������������� ![]() ���ɷ�����Ķ����֪��APB����BPC��120����Ȼ����֤����PAB����PBC����֤����ABP�ס�BCP ���ɢٿ�֪��ABP�ס�BCP���õ�
���ɷ�����Ķ����֪��APB����BPC��120����Ȼ����֤����PAB����PBC����֤����ABP�ס�BCP ���ɢٿ�֪��ABP�ס�BCP���õ�![]() ���������
���������![]() �ij�.
�ij�.![]() ��ͼ
��ͼ![]() ��ʾ��������֤����ACE�ա�ADB�����1����2���ɡ�3����4�ɵõ���CPD����5��60��.
��ʾ��������֤����ACE�ա�ADB�����1����2���ɡ�3����4�ɵõ���CPD����5��60��.
���ɡ�CPD��60��.��֤����BPC��180������CPD��120����Ȼ��֤����ADF�ס�PCF�������������ε����ʺ��ж�������֤����AFP�ס�DFC���ʴ˿ɵõ���APF����ACD��60����Ȼ�����á�APC����CPD����APF��120��������������á�APB��360������BPC����APC��120��,����˵��.
���������
(1)�١ߡ�PAB����PBA��180������APB��60������PBC����PBA����ABC��60����
���PAB����PBC.
�֡ߡ�APB����BPC��120����
���ɢٿ�֪��ABP�ס�BCP��
��![]()
��PB2��PA��PC��12��
![]()
(2)����ͼ���ߡ�ABE����ACD���������Σ�
��AE��AB��AC��AD����EAB����5��60��.
�ߡ�EAC����EAB����BAC����BAD����BAC����5��
���EAC����BAD��
���ACE�ա�ADB��
���1����2.
�ߡ�3����4��
���CPD����5��60��.
���ɢٿ�֪��1����2����3����4��
���ADF�ס�PCF��
��AF��PF��DF��CF��
��AF��DF��PF��CF.
�ߡ�AFP����CFD��
���AFP�ס�DFC��
���APF����ACD��60��.
�ɢٿ�֪��CPD��60����
���APC����CPD����APF��120����
��BPC��180������CPD��120����
���APB��360������BPC����APC��120����
���PΪ��ABC�ķ����㣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
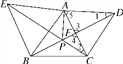
����Ŀ��ij����ƺ�ķ�������100����״��ͬ���������ι�����ɣ�Ϊ���ι������ÿ�λ�����Ҫ���0.4m����һ������ֵ�֧��������������ߵ��ײ�0.5m����ͼ������������������Ҫ�����֧�����ܳ�������Ϊ��������
A. 50m B. 100m C. 160m D. 200m
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
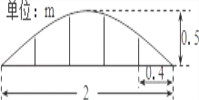
����Ŀ����ͼ���ס���Ϊ�������������֮���ˮƽ����BCΪ30m����A����D���������EADΪ45�㣬��B����D���������CBDΪ60�㣬��������������ĸ߶ȣ�����������ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�����������״Ϊֱ����������ͼ����������ͼ������ͼ��
(1)�벹�������ĸ���ͼ�������������ݣ�
(2)����ͼ������ijߴ�(��λ������)����������������ȫ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
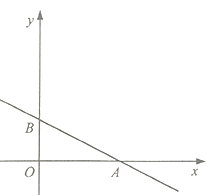
����Ŀ����ͼ��ֱ��![]() (
(![]() )��
)��![]() ���ڵ�
���ڵ�![]() ����
����![]() ���ڵ�
���ڵ�![]() .
.
(1)���![]() ������(�ú�
������(�ú�![]() �Ĵ���ʽ��ʾ)
�Ĵ���ʽ��ʾ)
(2)����![]() ��ֱ��
��ֱ��![]() �ϵ�����һ�㣬�ҵ�
�ϵ�����һ�㣬�ҵ�![]() ���
���![]() �������СֵΪ4�����ֱ�߱���ʽ��
�������СֵΪ4�����ֱ�߱���ʽ��
(3)��(2)�Ļ����ϣ�����![]() �ڵ�һ���ޣ���
�ڵ�һ���ޣ���![]() Ϊ����ֱ�������Σ����
Ϊ����ֱ�������Σ����![]() ������.
������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һλũ���������ǧ���Բ����������dz��ۣ�Ϊ�˷��㣬������һЩ��Ǯ���ã����г����۳�һЩ���ֽ��۳��ۣ��۳�������ǧ����x�������г��е�Ǯ��y����������Ǯ���Ĺ�ϵ��ͼ��ʾ�����ͼ��ش��������⣺

��1��ũ���Դ�����Ǯ�Ƕ��٣�
��2����ǰũ�����е�Ǯ��y���۳�������ǧ����x�ĺ�����ϵʽ��
��3�����ۺ�����ÿǧ��0.4Ԫ��ʣ���������꣬��ʱ�����е�Ǯ����������Ǯ����26Ԫ��������һ�����˶���ǧ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
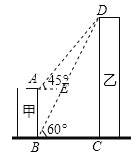
����Ŀ����ͼ��ij��ѧ��ȤС�������һ����CD�ĸ߶ȣ��������ڵ�A���������C������Ϊ30�㣬Ȼ����AD����ǰ��10m������B�㣬��B���������C�����Ǹ߶�Ϊ60�㣨A��B��D������ͬһֱ���ϣ�������������Dz������ݼ��������CD�ĸ߶ȣ������ȷ��0.1m�������ο����ݣ�![]() ��1.414��
��1.414��![]() ��1.732��
��1.732��
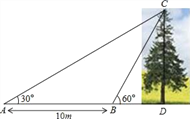
���𰸡�8.7��
������������������������������ε���ǵ����������ACB�Ķ������õ�BC�ij��ȣ�Ȼ����ֱ����BDC�У��������Ǻ���������⣮
����������ߡ�CBD=��A+��ACB��
���ACB=��CBD����A=60�㩁30��=30����
���A=��ACB��
��BC=AB=10���ף���
��ֱ����BCD�У�CD=BCsin��CBD=10��![]() =5
=5![]() ��5��1.732=8.7���ף���
��5��1.732=8.7���ף���
�������CD�ĸ߶�Ϊ8.7�ף�
���㣺��ֱ�������ε�Ӧ��
�����͡������
��������
23
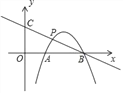
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������y=��x2+ax+b��x����A��1��0����B��3��0�����㣬��P�����������ڵ�һ�����ڵ�һ�㣬ֱ��BP��y���ཻ�ڵ�C��
��1����������y=��x2+ax+b�Ľ���ʽ��
��2������P���߶�BC���е�ʱ�����P�����ꣻ
��3���ڣ�2���������£���sin��OCB��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
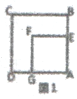
����Ŀ��������Դ��̽����С��������ѧ̽��������߳�Ϊa��������ABCD�ͱ߳���b��������AEFG��a>b��,��ʼʱ��E��AB�ϣ���ͼ1����������AEFG�Ƶ�A��ʱ�뷽����ת��
��1����ͼ2��С����������AEFG�Ƶ�A˳ʱ�뷽����ת������BE��DG����֤������ADG�ա�ABE��
��2����ͼ3��С����������AEFG�Ƶ�A˳ʱ�뷽����ת������BE��DG������Gǡ�������߶�BE�ϣ���a=3,b=2ʱ������������ʱDG�ij���
��3����ͼ4��С����ת������AEFG������E��DA���ӳ�����ʱ������BF��DF����FGƽ����BFD�����������a��b��ֵ.


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
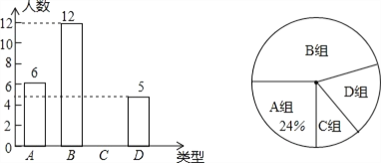
����Ŀ��Ϊ�˽�ѧ�����������ij��Բμ�A�飺�滭��B�飺�鷨��C�飺�赸��D�飺���������ĸ�������ȤС�����Ա�ֲ�������г������飬�������ռ������ݻ�������ͼ������������ͳ��ͼ�������ͼ���ṩ��Ϣ�������������⣺
(1)�˴ι������˶�����ͬѧ?
(2)������ͳ��ͼ����������
(3)��������ͳ��ͼ���鷨���ֵ�Բ�ĽǵĶ�����
(4)��֪�ڴ˴ε����У��μ�D���5��ѧ������3��Ů����2��������Ҫ����5��ѧ���������ȡ2��ѧ���μ��оٰ�������������б�������״ͼ�ķ��������ȡ��2��ѧ��ǡ����1��1Ů�ĸ��ʡ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com