

分析 (1)如图,作辅助线;证明∠BOC=30°,OB=2,借助直角三角形的边角关系即可解决问题;
(2)证明△APO≌△AQB,得到∠ABQ=∠AOP=90°,即可解决问题;
(3)根据点P在x的正半轴还是负半轴两种情况讨论,再根据全等三角形的性质即可得出结果.
解答  解:(1)如图1,过点B作BC⊥x轴于点C,
解:(1)如图1,过点B作BC⊥x轴于点C,
∵△AOB为等边三角形,且OA=2,
∴∠AOB=60°,OB=OA=2,
∴∠BOC=30°,而∠OCB=90°,
∴BC=$\frac{1}{2}$OB=1,OC=$\sqrt{3}$,
∴点B的坐标为B($\sqrt{3}$,1);
(2)∠ABQ=90°,始终不变.理由如下:
∵△APQ、△AOB均为等边三角形,
∴AP=AQ、AO=AB、∠PAQ=∠OAB,
∴∠PAO=∠QAB,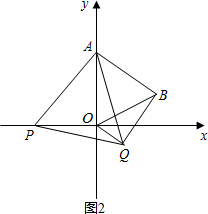
在△APO与△AQB中,
$\left\{\begin{array}{l}{AP=AQ}\\{∠PAO=∠QAB}\\{AO=AB}\end{array}\right.$,
∴△APO≌△AQB(SAS),
∴∠ABQ=∠AOP=90°;
(3)当点P在x轴负半轴上时,点Q在点B的下方,
∵AB∥OQ,∠BQO=90°,∠BOQ=∠ABO=60°.
又OB=OA=2,可求得BQ=$\sqrt{3}$,
由(2)可知,△APO≌△AQB,
∴OP=BQ=$\sqrt{3}$,
∴此时P的坐标为(-$\sqrt{3}$,0).
点评 本题主要考查了等边三角形的性质以及全等三角形的判定及性质以及梯形的性质,注意利用分类讨论得出是解题关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
| 车型 | 甲 | 乙 | 丙 |
| 汽车运载量(吨/辆) | 5 | 8 | 10 |
| 汽车运费(元/辆) | 400 | 500 | 600 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | $\frac{2}{3}$ | C. | -$\frac{3}{2}$ | D. | -$\frac{2}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 (1)计算:$\frac{2}{1+tan60°}$+|$\sqrt{3}$-2|
(1)计算:$\frac{2}{1+tan60°}$+|$\sqrt{3}$-2|查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com