
【题目】已知抛物线![]() 与x轴交于A.B两点,与y轴交于C点,抛物线的顶点为D点,点A的坐标为(﹣1,0).
与x轴交于A.B两点,与y轴交于C点,抛物线的顶点为D点,点A的坐标为(﹣1,0).
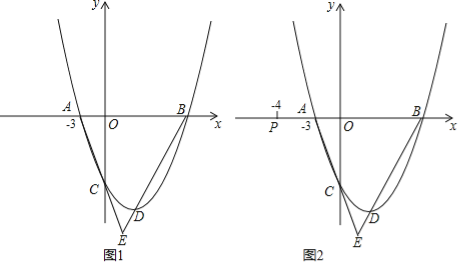
(1)求D点的坐标;
(2)如图1,连接AC,BD并延长交于点E,求∠E的度数;
(3)如图2,已知点P(﹣4,0),点Q在x轴下方的抛物线上,直线PQ交线段AC于点M,当∠PMA=∠E时,求点Q的坐标.
【答案】(1)顶点D的坐标为(1,﹣4)。
(2)∠E=45°
(3)点Q的坐标为(2,﹣3)或(![]() ,
,![]() )。
)。
【解析】
(1)将点A的坐标代入到抛物线的解析式求得c值,然后配方后即可确定顶点D的坐标。
(2)连接CD、CB,过点D作DF⊥y轴于点F,首先求得点C的坐标,然后证得△DCB∽△AOC得到∠CBD=∠OCA,根据∠ACB=∠CBD+∠E=∠OCA+∠OCB,得到∠E=∠OCB=45°。
(3)设直线PQ交y轴于N点,交BD于H点,作DG⊥x轴于G点,增大△DGB∽△PON后利用相似三角形的性质求得ON的长,从而求得点N的坐标,进而求得直线PQ的解析式,设Q(m,n),根据点Q在直线PQ和抛物线![]() 上,得到
上,得到![]() ,求得m、n的值后即可求得点Q的坐标。
,求得m、n的值后即可求得点Q的坐标。
解:(1)把x=﹣1,y=0代入![]() 得:1+2+c=0,∴c=﹣3。
得:1+2+c=0,∴c=﹣3。
∴![]() 。
。
∴顶点D的坐标为(1,﹣4)。
(2)如图1,连接CD、CB,过点D作DF⊥y轴于点F,
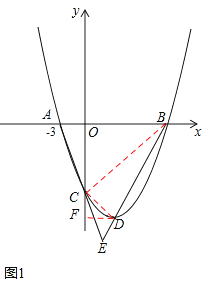
由![]() 解得x=﹣1或x=3,∴B(3,0)。
解得x=﹣1或x=3,∴B(3,0)。
当x=0时,![]() ,∴C(0,﹣3)。
,∴C(0,﹣3)。
∴OB=OC=3。
∵∠BOC=90°,∴∠OCB=45°,BC=![]() 。
。
又∵DF=CF=1,∠CFD=90°,
∴∠FCD=45°,CD=![]() 。
。
∴∠BCD=180°﹣∠OCB﹣∠FCD=90°
∴∠BCD=∠COA。
又∵![]() ,∴△DCB∽△AOC。
,∴△DCB∽△AOC。
又∵∠ACB=∠CBD+∠E=∠OCA+∠OCB,∴∠E=∠OCB=45°。
(3)如图2,设直线PQ交y轴于N点,交BD于H点,作DG⊥x轴于G点,
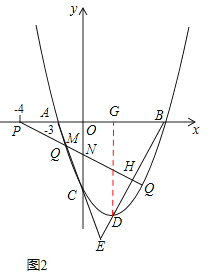
∵∠PMA=45°,∴∠EMH=45°。∴∠MHE=90°。
∴∠PHB=90°。∴∠DBG+∠OPN=90°。
又∵∠ONP+∠OPN=90°,∴∠DBG=∠ONP。
又∵∠DGB=∠PON=90°,∴△DGB=∠PON=90°。
∴△DGB∽△PON。
∴![]() ,即
,即![]() ,解得ON=2。
,解得ON=2。
∴N(0,﹣2)。
设直线PQ的解析式为y=kx+b,
则![]() ,解得:
,解得: 。
。
∴直线PQ的解析式为![]() 。
。
设Q(m,n)且n<0,∴![]() 。
。
又∵Q(m,n)在![]() 上,∴
上,∴![]() 。
。
∴![]() ,解得:m=2或m=
,解得:m=2或m=![]() 。
。
∴n=﹣3或n=![]() 。
。
∴点Q的坐标为(2,﹣3)或(![]() ,
,![]() )。
)。


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源: 题型:
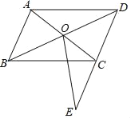
【题目】如图,在ABCD中,对角线AC、BD相交于点O,在DC的延长线上取一点E,连接OE交BC于点F,已知AB=6,BC=8,CE=2
(1)求CF的长.
(2)设△COF的面积为S1,△COD的面积为S2,直接写出S1:S2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() ,连接
,连接![]() ,
,![]() 为一动点.
为一动点.
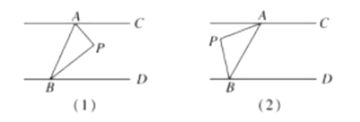
(1)当动点![]() 落在如图
落在如图![]() 所示的位置时,连接
所示的位置时,连接![]() ,求证:
,求证:![]() ;
;
(2)当动点![]() 落在如图
落在如图![]() 所示的位置时,连接
所示的位置时,连接![]() ,则
,则![]() 之间的关系如何,你得出的结论是 .(只写结果,不用写证明)
之间的关系如何,你得出的结论是 .(只写结果,不用写证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A,B两点的坐标分别是(0,4),(0,﹣4),点C是x轴上一个动点,过点B作直线BH⊥AC于点H,过点C作CD∥y轴,交BH于点D,点C在x轴上运动的过程中,点D不可能经过的点是( )
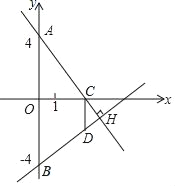
A. (2,﹣3) B. (1,﹣3) C. (4,0) D. (0,﹣4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.△ABC的三个顶点A,B,C都在格点上.将△ABC绕点A按顺时针方向旋转90°得到△AB′C′.
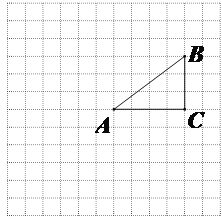
(1)在正方形网格中,画出△AB′C′;
(2)计算线段AB在变换到AB′的过程中扫过的区域的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c,自变量x与函数y的对应值如表:
x | … | ﹣5 | ﹣4 | ﹣3 | ﹣2 | ﹣1 | 0 | … |
y | … | 4 | 0 | ﹣2 | ﹣2 | 0 | 4 | … |
下列说法正确的是( )
A. 抛物线的开口向下
B. 当x>﹣![]() 时,y随x的增大而增大
时,y随x的增大而增大
C. 二次函数的最小值是﹣2
D. 抛物线的对称轴是x=1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题6分)为了参加中考体育测试,甲,乙,丙三位同学进行足球传球训练。球从一个人
脚下随机传到另一个人脚下,且每位传球人传球给其余两人的机会是均等的,由甲开始传球,共传三次。
(1)求请用树状图列举出三次传球的所有可能情况;
(2)传球三次后,球回到甲脚下的概率;
(3)三次传球后,球回到甲脚下的概率大还是传到乙脚下的概率大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年10月,吉州区井冈蜜柚节迎来了四方游客,游客李先生选购了井冈蜜柚和井冈板栗各一箱需要200元.他还准备给4位朋友每人送同样的井冈蜜柚一箱,6位同事每人送同样的井冈板栗一箱,就还需要1040元.
(1)求每箱井冈蜜柚和每箱井冈板栗各需要多少元?
(2)李先生到收银台才得知井冈蜜柚节期间,井冈蜜柚可以享受6折优惠,井冈板栗可以享受8折优惠,此时李先生比预计的付款少付了多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
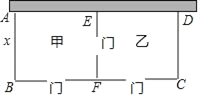
【题目】林场要建一个果园(矩形ABCD),果园的一面靠墙(墙最大可用长度为30米),另三边用木栏围成,中间EF也用木栏隔开,分为甲、乙两个场地,并在如图所示的三处各留1米宽的门(不用木栏),木栏总长57米.设果园(矩形ABCD)的宽AB为x米,矩形ABCD的面积为S平方米.
(1)求S关于x的函数表达式,并写出自变量x的取值范围.
(2)求果园能达到的最大面积S及相应x的值.
(3)若木栏BF比CF多10米,其余条件不变,甲场地种植葡萄,一季平均每平方米收益40元;乙场地种植益莓,一季平均每平方米收益160元.问该果园一季能达到的最大收益W为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com