练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    数学课上，老师用多媒体给同学们放了由魔术界当红艺人刘谦表演的的神奇的障眼法“硬币穿玻璃”魔术，敏捷的身手、幽默的语言把同学们逗得乐不可支。看完后老师说：“今天我也来当一回魔术师给你们现场表演一个数学魔术。”说完便在黑板上画出下面两个图：

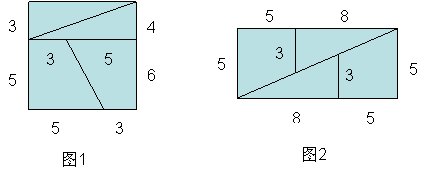
    请你借助数学知识帮助同学们分析老师画的这两个图，通过计算验证说明图1到图2的拼接是否可行，若不行请说明理由，并画出正确的拼接图  


    不可以。因为图1正方形的面积是64，而图2的矩形面积是65，所以不可能拼接好。利用三角形的相似，可以求出中间的平行四边形即为多出的面积1，正确的图为：


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    已知抛物线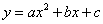的对称轴为直线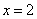，且与x轴交于A、B两点，与y轴交于点C，其中A(1，0)，C(0，-3).

    （1）求抛物线的解析式；

    （2）若点P在抛物线上运动（点P异于点A），

    ①如图1，当△PBC的面积与△ABC的面积相等时，求点P的坐标；

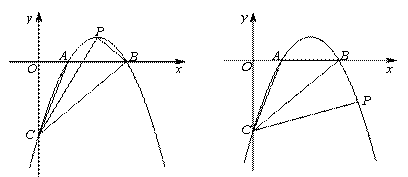    ②如图2，当∠PCB =∠BCA时，求直线CP的解析式．

    图1                          图2

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    将点A(2，1)向上平移3个单位长度得到点B的坐标是     ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    有两个圆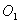，⊙的半径等于地球的半径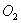，⊙的半径等于一个篮球的半径，现将两个圆都向外膨胀（相当于作同心圆），使周长都增加1米，则半径伸长的较多的圆是（   ）

    A、⊙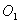   B、⊙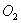  C、两圆的半径伸长是相同的 D、无法确定

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    正方形ABCD的边长为acm，E、F分别是BC、CD的中点，连接BF、DE，则图中阴影部分的面积是          cm2．

     


    查看答案和解析>>

    科目：初中数学 来源： 题型：


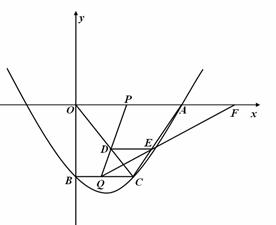
    如图,在平面直角坐标系xoy中,抛物线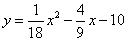与x轴,y轴的交点分别为点A,点B,过点B作x轴的平行线BC,交抛物线于点C,连结AC．现有两动点P,Q分别从O,C两点同时出发,点P以每秒4个单位的速度沿OA向终点A移动,点Q以每秒1个单位的速度沿CB向点B移动,点P停止运动时,点Q也同时停止运动,线段OC,PQ相交于点D,过点D作DE∥OA,交CA于点E,射线QE交x轴于点F．设动点P,Q移动的时间为t(单位:秒)

    (1)求A,B,C三点的坐标和抛物线的顶点的坐标;

    (2)当t为何值时,四边形PQCA为平行四边形?请写出计算过程;

    (3)当0＜t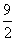＜时,△PQF的面积是否总为定值?若是,求出此定值,若不是,请说明理由;

    (4)当t为何值时,△PQF为等腰三角形?请写出解答过程．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    下列命题中，是真命题的是（    ）

    A．一组邻边相等的平行四边形是正方形；

    B．依次连结四边形四边中点所组成的图形是平行四边形；

    C．平分弦的直径垂直于弦，并且平分弦所对的弧；

    D．相等的圆心角所对的弧相等，所对的弦也相等；

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    新华社3月5日报道，中国计划将2014年国防预算提高12%，达到约8082亿元人民币，将8082亿用科学计数法表示应为（     ）（原创）

    A、80.82×1010       B、8.082×103        C、8.082×1011       D、0.8082×1012

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    2014年全国两会在京召开，公众最关心哪些问题？901班学生就老百姓最关注的两会热点问题，在网络上发布了相应的调查问卷。到目前为止，共有不同年龄段的2880人参与，具体情况统计如下：（原创）

    抽取的30-35岁人群的关注情况

    关心问题

    频数

    频率

    收入分配

    90

    0.25

    住房问题

    0.15

    物价调控

    36

    0.1

    医疗改革

    18

    养老保险

    0.15

    其他

    108

    合计

    360

    1

       所调查的2880人年龄分布情况

     

     

     

     

     

     


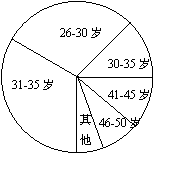    （1）请将统计表中遗漏的数据补上；

    （2）扇形图中表示30-35岁的扇形的圆心角是多少度？

    （3）在参加调查的30-35岁段中随机抽取一人，关心物价调控或医疗改革的概率是多少？

    （4）从上表中，你还能获得其它的信息吗?（写出一条即可）

    查看答案和解析>>

    同步练习册答案