练习册

  • 练习册
  • 试题
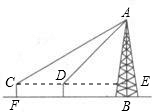
    精英家教网 > 初中数学 > 题目详情
    精英家教网如图，为了测量电视塔AB的高度，在C、D两点测得塔顶A的仰角分别为30°，45°．已知C、D两点在同一水平线上，C、D间的距离为60米，测倾器CF的高为1.5米，求电视塔AB的高．（精确到0.1米）
    分析：根据AE和∠ADE、AE和∠ACE可以求得DE、CE的长度，根据CD=CE-DE可以求出AE的长度，即可解题．
    解答：解：在Rt△ADE中，DE=
    AE
    tan45°
    =AE，
    Rt△ACE中，CE=
    AE
    tan30°
    =
    		3
    AE，
    ∵CD=CE-DE，
    ∴AE=
    CD
    		3
    -1
    =30（
    		3
    +1）米=81.96米
    所以电视塔高为81.96米+1.5米=83.46米≈83.5米．
    答：电视塔AB的高约83.5米．
    点评：本题考查了特殊角的三角函数值，考查了三角函数在直角三角形中的应用，本题中求DE、CE的长度是解题的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    91、如图，为了测量某电视塔的高度，在离电阻墙202m的D处，用测角仪测得塔顶A的仰角为47°，已知测角仪的高CD=1.4m，则电视塔的高度AB为
    218.0
    m．（结果精确到0.1m）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

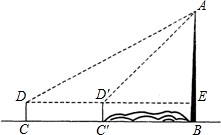    精英家教网如图，为了测量河对岸的电视塔AB的高度，在D处用测角仪溅得点A的仰角为30°，前进80米，在D′处测得点A的仰角为45°，已知测角仪CD=C′D′=1.2米，求电视塔AB的高度（
    		3
    ≈1.73，精确到1米）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

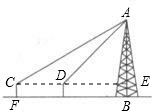    如图，为了测量电视塔AB的高度，在C、D两点测得塔顶A的仰角分别为30°，45°．已知C、D两点在同一水平线上，C、D间的距离为60米，测倾器CF的高为1.5米，求电视塔AB的高．（精确到0.1米）

    查看答案和解析>>

    科目：初中数学 来源：《31.3 锐角三角函数的应用》2010年习题精选（解析版） 题型：解答题

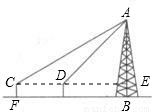
    如图，为了测量电视塔AB的高度，在C、D两点测得塔顶A的仰角分别为30°，45°．已知C、D两点在同一水平线上，C、D间的距离为60米，测倾器CF的高为1.5米，求电视塔AB的高．（精确到0.1米）

    查看答案和解析>>

    同步练习册答案