已知:抛物线y=x2+(b-1)x+c经过点P(-1,-2b).
(1)求b+c的值;
(2)若b=3,求这条抛物线的顶点坐标;
(3)若b>3,过点P作直线PA⊥y轴,交y轴于点A,交抛物线于另一点B,且BP=2PA,求这条抛物线所对应的二次函数关系式.(提示:请画示意图思考)
【答案】
分析:(1)因为抛物线y=x
2+(b-1)x+c经过点P(-1,-2b),所以将点P代入解析式即可求得;
(2)因为b=3,所以求得c的值,即可求得抛物线的解析式,然后利用配方法求出顶点坐标;
(3)解此题的关键是首先确定函数的草图,即开口方向是向上,对称轴为x=
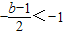
,在y轴的左侧,根据题意确定点B的坐标;因为点P与点B关于对称轴对称,所以确定对称轴方程,从而求得b、c的值,求得函数解析式.
解答: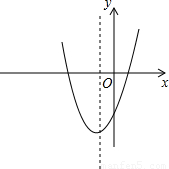
解:(1)依题意得:(-1)
2+(b-1)(-1)+c=-2b (2分)
∴b+c=-2.(3分)
(2)当b=3时,c=-5,(4分)
∴y=x
2+2x-5=(x+1)
2-6,
∴抛物线的顶点坐标是(-1,-6).(6分)
(3)当b>3时,抛物线对称轴x=
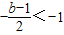
∴对称轴在点P的左侧
因为抛物线是轴对称图形,P(-1,-2b)且BP=2PA
∴B(-3,-2b) (9分)
∴
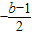
=-2,
∴b=5 (10分)
又b+c=-2,
∴c=-7 (11分)
∴抛物线所对应的二次函数关系式为y=x
2+4x-7. (12分)
解法2:(3)
当b>3时,-b<-3,1-b<-2,则x=-
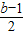
=
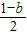
<-1,
∴对称轴在点P的左侧,因为抛物线是轴对称图形
∵P(-1,-2b),且BP=2PA,
∴B(-3,-2b) (9分)
∴(-3)
2-3(b-1)+c=-2b(10分)
又b+c=-2,
解得b=5,c=-7(11分)
这条抛物对应的二次函数关系式为y=x
2+4x-7.(12分)
解法3:(3)∵b+c=-2,
∴c=-b-2
∴y=x
2+(b-1)x-b-2( 7分)
BP∥x轴,
∴x
2+(b-1)x-b-2=-2b( 8分)
即x
2+(b-1)x+b-2=0
解得:x
1=-1,x
2=-(b-2),即x
B=-(b-2)10分
由BP=2PA,
∴-1+(b-2)=2×1
∴b=5,c=-7 (11分)
∴抛物线所对应的二次函数关系式为y=x
2+4x-7.(12分)
点评:此题考查了待定系数法求函数的解析式,考查了二次函数的对称性,解题的关键是要注意数形结合思想的应用.

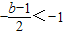 ,在y轴的左侧,根据题意确定点B的坐标;因为点P与点B关于对称轴对称,所以确定对称轴方程,从而求得b、c的值,求得函数解析式.
,在y轴的左侧,根据题意确定点B的坐标;因为点P与点B关于对称轴对称,所以确定对称轴方程,从而求得b、c的值,求得函数解析式. 解:(1)依题意得:(-1)2+(b-1)(-1)+c=-2b (2分)
解:(1)依题意得:(-1)2+(b-1)(-1)+c=-2b (2分)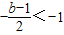
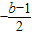 =-2,
=-2,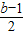 =
=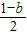 <-1,
<-1,

 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案