
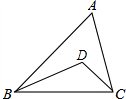
 在△ABC中,∠A=50°,D点时∠ABC和∠ACB角平分线的交点,则∠BDC=115°.
在△ABC中,∠A=50°,D点时∠ABC和∠ACB角平分线的交点,则∠BDC=115°.  天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
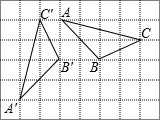 如图,在正方形网格中,每个小正方形的边长均为1,△ABC和△A′B′C′的各个顶点均在格点处,且△A′B′C′是由△ABC以网格中的某个格点为旋转中心,逆时针旋转90°得到的,点A,B,C的对应点分别为点A′,B′,C′,则在旋转过程中,点A经过的路径长为( )
如图,在正方形网格中,每个小正方形的边长均为1,△ABC和△A′B′C′的各个顶点均在格点处,且△A′B′C′是由△ABC以网格中的某个格点为旋转中心,逆时针旋转90°得到的,点A,B,C的对应点分别为点A′,B′,C′,则在旋转过程中,点A经过的路径长为( )| A. | $\frac{\sqrt{10}}{4}$π | B. | $\frac{\sqrt{13}}{2}$π | C. | $\frac{\sqrt{13}}{4}$π | D. | $\frac{\sqrt{10}}{2}$π |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在矩形ABCD中,AB=2,BC=4,点M、N分别在边AD和BC上,沿MN折叠四边形ABCD,使点A、B分别落在A1、B1处,得四边形A1B1NM,其中点B1在DC上,过点M作ME⊥BC于点E,连接BB1,给出下列结论:①∠MNB1=∠ABB1;②△MEN∽△BCB1;③$\frac{MN}{B{B}_{1}}$的值为定值;④当B1C=$\frac{1}{2}$DC时,AM=$\frac{17}{8}$,其中正确结论的序号是①②③.(把所有正确结论的序号都在填在横线上)
如图,在矩形ABCD中,AB=2,BC=4,点M、N分别在边AD和BC上,沿MN折叠四边形ABCD,使点A、B分别落在A1、B1处,得四边形A1B1NM,其中点B1在DC上,过点M作ME⊥BC于点E,连接BB1,给出下列结论:①∠MNB1=∠ABB1;②△MEN∽△BCB1;③$\frac{MN}{B{B}_{1}}$的值为定值;④当B1C=$\frac{1}{2}$DC时,AM=$\frac{17}{8}$,其中正确结论的序号是①②③.(把所有正确结论的序号都在填在横线上)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 在长方形ABCD中,放入6个长度相同的小长方形,所标尺寸如图所示,设小长方形的宽AE=xcm,依题意可列方程( )
在长方形ABCD中,放入6个长度相同的小长方形,所标尺寸如图所示,设小长方形的宽AE=xcm,依题意可列方程( )| A. | 6+2x=14-3x | B. | 6+2x=x+(14-3x) | C. | 6+2x=14-x | D. | 14-3x=6+2x |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5 | B. | 2 | C. | $\frac{2}{5}$ | D. | $\frac{5}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com