
”¾ĢāÄæ”æĪŖČ«ĆęĶĘ½ų”°Čż¹©Ņ»Ņµ”±·ÖĄėŅĘ½»¹¤×÷£¬¼×”¢ŅŅĮ½øö¹¤³Ģ¶Ó³ŠĄæĮĖijÉēĒų2400Ć׵ĵēĀ·¹ÜµĄĘĢÉč¹¤³Ģ£®ŅŃÖŖ¼×¶ÓĆæĢģĘĢÉč¹ÜµĄµÄ³¤¶ČŹĒŅŅ¶ÓĆæĢģĘĢÉč¹ÜµĄ³¤¶ČµÄ1£®5±¶£¬ČōĮ½¶Óø÷×Ō¶ĄĮ¢Ķź³É1200Ć×µÄĘĢÉčČĪĪń£¬Ōņ¼×¶Ó±ČŅŅ¶ÓÉŁÓĆ10Ģģ£®
£Ø1£©Ēó¼×”¢ŅŅĮ½¹¤³Ģ¶ÓĆæĢģ·Ö±šĘĢÉčµēĀ·¹ÜµĄ¶ąÉŁĆ×£»
£Ø2£©Čō¼×¶Ó²ĪÓėøĆĻī¹¤³ĢµÄŹ©¹¤Ź±¼ä²»µĆ³¬¹ż20Ģģ£¬ŌņŅŅ¶ÓÖĮÉŁŹ©¹¤¶ąÉŁĢģ²ÅÄÜĶź³ÉøĆĻī¹¤³Ģ£æ
”¾“š°ø”æ£Ø1£©¼×”¢ŅŅĮ½¹¤³Ģ¶ÓĆæĢģ·Ö±šĘĢÉčµēĀ·¹ÜµĄ60Ć×”¢40Ć×£»£Ø2£©Čō¼×¶Ó²ĪÓėøĆĻī¹¤³ĢµÄŹ©¹¤Ź±¼ä²»µĆ³¬¹ż20Ģģ£¬ŌņŅŅ¶ÓÖĮÉŁŹ©¹¤30Ģģ²ÅÄÜĶź³ÉøĆĻī¹¤³Ģ£®
”¾½āĪö”æ
£Ø1£©ÉčŅŅ¶ÓĆæĢģĘĢÉčµēĀ·¹ÜµĄ![]() Ć×£¬øł¾ŻĮ½¶Óø÷×Ō¶ĄĮ¢Ķź³É1200Ć×µÄĘĢÉčČĪĪń£¬Ōņ¼×¶Ó±ČŅŅ¶ÓÉŁÓĆ10Ģģ£¬ĮŠ·½³ĢĒó½ā¼“æÉ£»
Ć×£¬øł¾ŻĮ½¶Óø÷×Ō¶ĄĮ¢Ķź³É1200Ć×µÄĘĢÉčČĪĪń£¬Ōņ¼×¶Ó±ČŅŅ¶ÓÉŁÓĆ10Ģģ£¬ĮŠ·½³ĢĒó½ā¼“æÉ£»
£Ø2£©ÉčŅŅ¶ÓŹ©¹¤![]() ĢģÕżŗĆĶź³ÉøĆĻī¹¤³Ģ£¬øł¾Ż¼×¶Ó²ĪÓėøĆĻī¹¤³ĢµÄŹ©¹¤Ź±¼ä²»µĆ³¬¹ż20Ģģ£¬ĮŠ²»µČŹ½Ēó½ā¼“æÉ£®
ĢģÕżŗĆĶź³ÉøĆĻī¹¤³Ģ£¬øł¾Ż¼×¶Ó²ĪÓėøĆĻī¹¤³ĢµÄŹ©¹¤Ź±¼ä²»µĆ³¬¹ż20Ģģ£¬ĮŠ²»µČŹ½Ēó½ā¼“æÉ£®
½ā£ŗ£Ø1£©ÉčŅŅ¶ÓĆæĢģĘĢÉčµēĀ·¹ÜµĄ![]() Ć×£¬Ōņ¼×¶ÓĆæĢģĘĢÉčµēĀ·¹ÜµĄ
Ć×£¬Ōņ¼×¶ÓĆæĢģĘĢÉčµēĀ·¹ÜµĄ![]() Ć×£¬
Ć×£¬
øł¾ŻĢāŅā£¬µĆ![]() £¬
£¬
½āµĆ![]() £¬
£¬
¾¼ģŃ飬![]() ŹĒĖłĮŠ·½³ĢµÄ½ā£¬“ĖŹ±£¬
ŹĒĖłĮŠ·½³ĢµÄ½ā£¬“ĖŹ±£¬![]() £¬
£¬
“š£ŗ¼×”¢ŅŅĮ½¹¤³Ģ¶ÓĆæĢģ·Ö±šĘĢÉčµēĀ·¹ÜµĄ60Ć×”¢40Ć×£»
£Ø2£©ÉčŅŅ¶ÓŹ©¹¤![]() ĢģÕżŗĆĶź³ÉøĆĻī¹¤³Ģ£¬
ĢģÕżŗĆĶź³ÉøĆĻī¹¤³Ģ£¬
øł¾ŻĢāŅā£¬µĆ![]() £¬
£¬
½āµĆ![]() £¬
£¬
“š£ŗČō¼×¶Ó²ĪÓėøĆĻī¹¤³ĢµÄŹ©¹¤Ź±¼ä²»µĆ³¬¹ż20Ģģ£¬ŌņŅŅ¶ÓÖĮÉŁŹ©¹¤30Ģģ²ÅÄÜĶź³ÉøĆĻī¹¤³Ģ£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
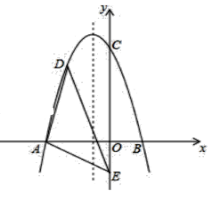
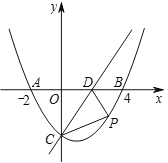
”¾ĢāÄæ”æČēĶ¼ĖłŹ¾£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬¶ž“ĪŗÆŹży£½ax2£«bx£«c½»xÖįÓŚA(£4,0)”¢B(2,0)£¬ŌŚyÖįÉĻÓŠŅ»µć E(0£¬£2)£¬Į¬½ÓAE£®
 ””””””””
””””””””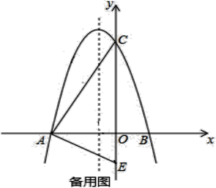
£Ø1£©Ē󶞓ĪŗÆŹżµÄ±ķ“ļŹ½£»
£Ø2£©µćDŹĒµŚ¶žĻóĻŽÄŚµÄÅ×ĪļĻßÉĻŅ»¶Æµć£®Čōtan”ĻAED£½![]() £¬Ēó“ĖŹ±µćD×ų±ź£»
£¬Ēó“ĖŹ±µćD×ų±ź£»
£Ø3£©Į¬½ÓAC£¬µćPŹĒĻ߶ĪCAÉĻµÄ¶Æµć£¬Į¬½ÓOP£¬°ŃĻ߶ĪPOČĘ×ŵćPĖ³Ź±ÕėŠż×Ŗ90”ćÖĮPQ£¬µćQŹĒµćOµÄ¶ŌÓ¦µć£®µ±¶ÆµćP“ÓµćCŌĖ¶Æµ½µćAŹ±£¬ÅŠ¶Ļ¶ÆµćQµÄ¹ģ¼£²¢Ēó¶ÆµćQĖł¾¹żµÄĀ·¾¶³¤£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖ£ŗŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬OĪŖ×ų±źŌµć£¬Å×ĪļĻßy£½ax2©2ax©3a·Ö±š½»xÖįÓŚA”¢BĮ½µć£ØµćAŌŚµćBµÄ²ą£©£¬ÓėyÖį½»ÓŚµćC£¬Į¬½ÓAC£¬tan”ĻACO£½![]() £®
£®
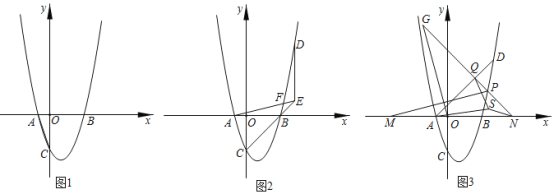
£Ø1£©ČēĶ¼l£¬ĒóaµÄÖµ£»
£Ø2£©ČēĶ¼2£¬DŹĒµŚŅ»ĻóĻŽÅ×ĪļĻßÉĻµÄµć£¬¹żµćD×÷yÖįµÄĘ½ŠŠĻß½»CBµÄŃÓ³¤ĻßÓŚµćE£¬Į¬½ÓAE½»BDÓŚµćF£¬AE£½BD£¬ĒóµćDµÄ×ų±ź£»
£Ø3£©ČēĶ¼3£¬ŌŚ£Ø2£©µÄĢõ¼žĻĀ£¬Į¬½ÓAD£¬PŹĒµŚŅ»ĻóĻŽÅ×ĪļĻßÉĻµÄµć£ØµćPÓėµćD²»ÖŲŗĻ£©£¬¹żµćP×÷ADµÄ“¹Ļߣ¬“¹×ćĪŖQ£¬½»xÖįÓŚµćN£¬µćMŌŚxÖįÉĻ£ØµćMŌŚµćNµÄ×ó²ą£©£¬µćGŌŚNPµÄŃÓ³¤ĻßÉĻ£¬MP£½OG£¬”ĻMPN©”ĻMOG£½45”ć£¬MN£½10![]() £®µćSŹĒ”÷AQNÄŚŅ»µć£¬Į¬½ÓAS”¢QS”¢NS£¬AS£½AQ£¬QS£½
£®µćSŹĒ”÷AQNÄŚŅ»µć£¬Į¬½ÓAS”¢QS”¢NS£¬AS£½AQ£¬QS£½![]() SN£¬ĒóQSµÄ³¤£®
SN£¬ĒóQSµÄ³¤£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ![]() ÖŠ£¬
ÖŠ£¬![]() £¬
£¬![]() £¬
£¬![]() £¬µć
£¬µć![]() ŹĒ
ŹĒ![]() µÄÖŠµć£¬µć
µÄÖŠµć£¬µć![]() ŹĒ±ß
ŹĒ±ß![]() ÉĻŅ»¶Æµć£¬ŃŲ
ÉĻŅ»¶Æµć£¬ŃŲ![]() ĖłŌŚÖ±Ļß°Ń
ĖłŌŚÖ±Ļß°Ń![]() ·ÕŪµ½
·ÕŪµ½![]() µÄĪ»ÖĆ£¬ČōĻ߶Ī
µÄĪ»ÖĆ£¬ČōĻ߶Ī![]() ½»
½»![]() ÓŚµć
ÓŚµć![]() £¬ĒŅ
£¬ĒŅ![]() ĪŖÖ±½ĒČż½ĒŠĪ£¬Ōņ
ĪŖÖ±½ĒČż½ĒŠĪ£¬Ōņ![]() µÄ³¤ĪŖ______£®
µÄ³¤ĪŖ______£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬Å×ĪļĻß![]() Óė
Óė![]() Öį½»ÓŚµć
Öį½»ÓŚµć![]() £¬
£¬![]() £¬ÓėÖ±Ļß
£¬ÓėÖ±Ļß![]() ½»ÓŚµć
½»ÓŚµć![]() £¬Ö±Ļß
£¬Ö±Ļß![]() Óė
Óė![]() Öį½»ÓŚµć
Öį½»ÓŚµć![]() £®
£®
(1)ĒóøĆÅ×ĪļĻߵĽāĪöŹ½£®
(2)µć![]() ŹĒÅ×ĪļĻßÉĻµŚĖÄĻóĻŽÉĻµÄŅ»øö¶Æµć£¬Į¬½Ó
ŹĒÅ×ĪļĻßÉĻµŚĖÄĻóĻŽÉĻµÄŅ»øö¶Æµć£¬Į¬½Ó![]() £¬
£¬![]() £¬µ±
£¬µ±![]() µÄĆ껿×ī“óŹ±£¬Ēóµć
µÄĆ껿×ī“óŹ±£¬Ēóµć![]() µÄ×ų±ź£®
µÄ×ų±ź£®
(3)½«Å×ĪļĻߵĶŌ³ĘÖįĻņ×óĘ½ŅĘ3øö³¤¶Čµ„Ī»µĆµ½Ö±Ļß![]() £¬µć
£¬µć![]() ŹĒÖ±Ļß
ŹĒÖ±Ļß![]() ÉĻŅ»µć£¬Į¬½Ó
ÉĻŅ»µć£¬Į¬½Ó![]() £¬
£¬![]() £¬ČōÖ±Ļß
£¬ČōÖ±Ļß![]() ÉĻ“ęŌŚŹ¹
ÉĻ“ęŌŚŹ¹![]() ×ī“óµÄµć
×ī“óµÄµć![]() £¬ĒėÖ±½ÓŠ“³öĀś×ćĢõ¼žµÄµć
£¬ĒėÖ±½ÓŠ“³öĀś×ćĢõ¼žµÄµć![]() µÄ×ų±ź£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
µÄ×ų±ź£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
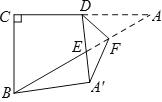
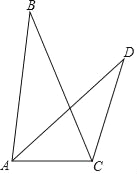
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ”÷ABCŗĶ”÷ACDÖŠ£¬”ĻB=”ĻD£¬tanB=![]() £¬BC=5£¬CD=3£¬”ĻBCA=90”ć©
£¬BC=5£¬CD=3£¬”ĻBCA=90”ć©![]() ”ĻBCD£¬ŌņAD=_____£®
”ĻBCD£¬ŌņAD=_____£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŌĻĀĖµ·ØÕżČ·µÄŹĒ(””””)
A.Š”Ć÷×öĮĖ![]() “ĪÖĄĶ¼¶¤µÄŹµŃ飬·¢ĻÖ
“ĪÖĄĶ¼¶¤µÄŹµŃ飬·¢ĻÖ![]() “Ī¶¤¼ā³ÆÉĻ£¬ÓÉ“ĖĖūĖµ¶¤¼ā³ÆÉĻµÄøÅĀŹŹĒ
“Ī¶¤¼ā³ÆÉĻ£¬ÓÉ“ĖĖūĖµ¶¤¼ā³ÆÉĻµÄøÅĀŹŹĒ![]()
B.Ņ»×é¶Ō±ßĘ½ŠŠ£¬ĮķŅ»×é¶Ō±ßĻąµČµÄĖıߊĪŹĒĘ½ŠŠĖıߊĪ
C.µć![]() ¶¼ŌŚ·“±ČĄżŗÆŹż
¶¼ŌŚ·“±ČĄżŗÆŹż![]() Ķ¼ĻóÉĻ£¬ĒŅ
Ķ¼ĻóÉĻ£¬ĒŅ![]() Ōņ
Ōņ![]() £»
£»
D.¶ŌÓŚŅ»ŌŖ¶žŌŖ·½³Ģ![]() £¬Čō
£¬Čō![]() Ōņ·½³ĢµÄĮ½øöøł»„ĪŖĻą·“Źż
Ōņ·½³ĢµÄĮ½øöøł»„ĪŖĻą·“Źż
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ![]() Äź³õ£¬Īäŗŗ±¬·¢ĮĖŠĀŠĶ¹Ś×“²”¶¾ŅżĘšµÄ·ĪŃ×£¬²¢ŃøĖŁŌŚČ«¹ś“«Č¾æŖĄ“£¬Óė“ĖĶ¬Ź±Ņ½»¤ČĖŌ±Ņ»Ö±¼įŹŲŌŚæ¹»÷·ĪŃ×µÄĒ°Ļߣ¬ĪŖĪŅĆĒ±£¼Ż»¤ŗ½£”ĀŽĀüĀŽĄ¼Ėµ£ŗ”°·²ŹĒŠŠĪŖÉĘĮ¼ÓėøßÉŠµÄČĖ£¬¶ØÄÜŅņÖ®¶ųµ£µ±»¼ÄŃ£®”±ĖūĆĒŹĒ×īæÉĒ×æɾ“µÄČĖ£”ÓÉ“Ė£¬Ņ½ĮĘĪļ׏»¤Äæ¾µµÄŠčĒóĮæ“ó“óŌö¼Ó£¬Į½½ŠĀĒųij»¤Äæ¾µÉś ²ś³§¼Ņ×ŌÕżŌĀ³õȿʚ±ćŅŖĒóČ«ĢåŌ±¹¤ĢįĒ°·µøŚ£¬ŌŚ½Óµ½µ„Ī»µÄ·µøŚĶØÖŖŗó£¬Ō±¹¤ĆĒ¶¼ŗĮĪŽŌ¹ŃŌ£¬æģĖŁ»Ųµ½ĮĖ×Ō¼ŗµÄ¹¤×÷øŚĪ»£¬ÓĆ×Ō¼ŗµÄŹµ¼ŹŠŠ¶Æ¼łŠŠ×ÅŅ»·ŻŌšČĪŗĶµ£µ±£®ŅŃÖŖøĆ³§ÓµÓŠĮ½Ģõ²»Ķ¬µÄ»¤Äæ¾µ¼Ó¹¤Éś²śĻß
Äź³õ£¬Īäŗŗ±¬·¢ĮĖŠĀŠĶ¹Ś×“²”¶¾ŅżĘšµÄ·ĪŃ×£¬²¢ŃøĖŁŌŚČ«¹ś“«Č¾æŖĄ“£¬Óė“ĖĶ¬Ź±Ņ½»¤ČĖŌ±Ņ»Ö±¼įŹŲŌŚæ¹»÷·ĪŃ×µÄĒ°Ļߣ¬ĪŖĪŅĆĒ±£¼Ż»¤ŗ½£”ĀŽĀüĀŽĄ¼Ėµ£ŗ”°·²ŹĒŠŠĪŖÉĘĮ¼ÓėøßÉŠµÄČĖ£¬¶ØÄÜŅņÖ®¶ųµ£µ±»¼ÄŃ£®”±ĖūĆĒŹĒ×īæÉĒ×æɾ“µÄČĖ£”ÓÉ“Ė£¬Ņ½ĮĘĪļ׏»¤Äæ¾µµÄŠčĒóĮæ“ó“óŌö¼Ó£¬Į½½ŠĀĒųij»¤Äæ¾µÉś ²ś³§¼Ņ×ŌÕżŌĀ³õȿʚ±ćŅŖĒóČ«ĢåŌ±¹¤ĢįĒ°·µøŚ£¬ŌŚ½Óµ½µ„Ī»µÄ·µøŚĶØÖŖŗó£¬Ō±¹¤ĆĒ¶¼ŗĮĪŽŌ¹ŃŌ£¬æģĖŁ»Ųµ½ĮĖ×Ō¼ŗµÄ¹¤×÷øŚĪ»£¬ÓĆ×Ō¼ŗµÄŹµ¼ŹŠŠ¶Æ¼łŠŠ×ÅŅ»·ŻŌšČĪŗĶµ£µ±£®ŅŃÖŖøĆ³§ÓµÓŠĮ½Ģõ²»Ķ¬µÄ»¤Äæ¾µ¼Ó¹¤Éś²śĻß![]() £®Ō¼Ę»®
£®Ō¼Ę»®![]() Éś²śĻßĆ抔Ź±Éś²ś»¤Äæ¾µ
Éś²śĻßĆ抔Ź±Éś²ś»¤Äæ¾µ![]() øö£¬
øö£¬![]() Éś²śĻßĆ抔Ź±Éś²ś»¤Äæ¾µ
Éś²śĻßĆ抔Ź±Éś²ś»¤Äæ¾µ![]() øö£®
øö£®
£Ø1£©ČōÉś²śĻß![]() Ņ»¹²¹¤×÷
Ņ»¹²¹¤×÷![]() Š”Ź±£¬ĒŅÉś²ś»¤Äæ¾µµÄ×ÜŹżĮæ²»ÉŁÓŚ
Š”Ź±£¬ĒŅÉś²ś»¤Äæ¾µµÄ×ÜŹżĮæ²»ÉŁÓŚ![]() øö£¬Ōņ
øö£¬Ōņ![]() Éś²śĻßÖĮÉŁÉś²ś»¤Äæ¾µ¶ąÉŁŠ”Ź±£æ
Éś²śĻßÖĮÉŁÉś²ś»¤Äæ¾µ¶ąÉŁŠ”Ź±£æ
£Ø2£©Ō¼Ę»®![]() Éś²śĻßĆæĢģ¾ł¹¤×÷
Éś²śĻßĆæĢģ¾ł¹¤×÷![]() Š”Ź±£¬µ«ĻÖŌŚĪŖĮĖ¾”æģĀś×ćĪŅŹŠ»¤Äæ¾µµÄŠčĒó£¬Į½ĢõÉś²śĻßĆæĢģ¾ł±ČŌ¼Ę»®¶ą¹¤×÷ĮĖĻąĶ¬µÄŠ”Ź±Źż£¬µ«ŅņĪŖ»śĘ÷Ėšŗļ°ČĖŌ±²»×ćŌŅņ£¬
Š”Ź±£¬µ«ĻÖŌŚĪŖĮĖ¾”æģĀś×ćĪŅŹŠ»¤Äæ¾µµÄŠčĒó£¬Į½ĢõÉś²śĻßĆæĢģ¾ł±ČŌ¼Ę»®¶ą¹¤×÷ĮĖĻąĶ¬µÄŠ”Ź±Źż£¬µ«ŅņĪŖ»śĘ÷Ėšŗļ°ČĖŌ±²»×ćŌŅņ£¬![]() Éś²śĻßĆæŌö¼Ó
Éś²śĻßĆæŌö¼Ó![]() Š”Ź±£¬øĆÉś²śĻßĆ抔Ź±µÄ²śĮ潫¼õÉŁ
Š”Ź±£¬øĆÉś²śĻßĆ抔Ź±µÄ²śĮ潫¼õÉŁ![]() øö£¬
øö£¬![]() Éś²śĻßĆæŌö¼Ó
Éś²śĻßĆæŌö¼Ó![]() Š”Ź±£¬øĆÉś²śĻßĆ抔Ź±µÄ²śĮ潫¼õÉŁ
Š”Ź±£¬øĆÉś²śĻßĆ抔Ź±µÄ²śĮ潫¼õÉŁ![]() øö£®ÕāŃłŅ»ĢģÉś²śµÄ»¤Äæ¾µ½«±ČŌ¼Ę»®¶ą
øö£®ÕāŃłŅ»ĢģÉś²śµÄ»¤Äæ¾µ½«±ČŌ¼Ę»®¶ą![]() øö£¬ĒóøĆ³§Źµ¼ŹĆæĢģÉś²ś»¤Äæ¾µµÄŹ±¼ä£®
øö£¬ĒóøĆ³§Źµ¼ŹĆæĢģÉś²ś»¤Äæ¾µµÄŹ±¼ä£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”ææĘ¼¼Š”×é½ųŠŠĮĖ»śĘ÷ČĖŠŠ×ߊŌŹµŃ飬ŌŚŹµŃé³”µŲÓŠ![]() ČżµćŌŚĶ¬Ņā±ŹÖ±µÄČüµĄÉĻ£¬
ČżµćŌŚĶ¬Ņā±ŹÖ±µÄČüµĄÉĻ£¬![]() Į½µćÖ®¼äµÄ¾ąĄėŹĒ540m£¬¼×”¢ŅŅĮ½»śĘ÷ČĖ·Ö±š“Ó
Į½µćÖ®¼äµÄ¾ąĄėŹĒ540m£¬¼×”¢ŅŅĮ½»śĘ÷ČĖ·Ö±š“Ó![]() Į½µć³ö·¢£¬¼×»śĘ÷ČĖŌČĖŁ°“
Į½µć³ö·¢£¬¼×»śĘ÷ČĖŌČĖŁ°“![]() µÄ·½ĻņŠŠ×ߣ¬ŅŅ»śĘ÷ČĖ°“
µÄ·½ĻņŠŠ×ߣ¬ŅŅ»śĘ÷ČĖ°“![]() ·½ĻņŠŠ×ߣ¬ŅŅĻČ³ö·¢1min£¬¼×ŌŁ³ö·¢£¬¼×”¢ŅŅĄėø÷×Ō³ö·¢µćµÄ¾ąĄė
·½ĻņŠŠ×ߣ¬ŅŅĻČ³ö·¢1min£¬¼×ŌŁ³ö·¢£¬¼×”¢ŅŅĄėø÷×Ō³ö·¢µćµÄ¾ąĄė![]() ÓėŅŅ³ö·¢µÄŹ±¼ä
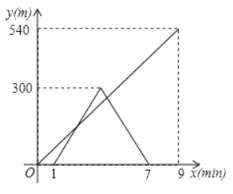
ÓėŅŅ³ö·¢µÄŹ±¼ä![]() µÄŗÆŹż¹ŲĻµŹ½ČēĶ¼ĖłŹ¾£¬½įŗĻĶ¼Ļń»Ų“šĻĀĮŠĪŹĢā£ŗ
µÄŗÆŹż¹ŲĻµŹ½ČēĶ¼ĖłŹ¾£¬½įŗĻĶ¼Ļń»Ų“šĻĀĮŠĪŹĢā£ŗ
£Ø1£©¼×µÄĖŁ¶ČŹĒ__________m/min£»ŅŅµÄĖŁ¶ČŹĒ________m/min;
£Ø2£©Ēó¼×»śĘ÷ČĖ“ÓCµć·µ»ŲAµćŹ±![]() Óė
Óė![]() µÄŗÆŹż¹ŲĻµŹ½£»
µÄŗÆŹż¹ŲĻµŹ½£»
£Ø3£©ŅŅ»śĘ÷ČĖ³ö·¢¶ą³¤Ź±¼äŗóĮ½»śĘ÷ČĖĻą¾ą80m.
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com