
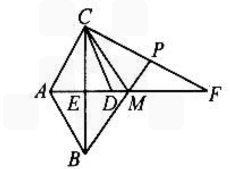
(1)证明:∵AF平分∠BAC,
∴∠CAD= ∠DAB=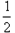 ∠BAC.
∠BAC.
∵点D与点A关于点E对称∴E为AD中点. BC⊥AD,
∴BC为AD的中垂线,
∴AC= CD
∵在Rt△ACE和Rt△ABE中,∠CAD+∠ACE=∠DAB+ ∠ABE = .∠CAD= ∠DAB.
.∠CAD= ∠DAB.
∴∠ACE= ∠ABE,
∴AC =AB,
∴AB= CD.
(2)∵∠BAC =2∠MPC,
又∵∠BAC =2∠CAD,
∴∠MPC=∠CAD.
∵AC= CD,
∴∠CAD=∠CDA,
∵∠MPC=∠CDA.
∴∠MPF=∠CDM,
∵AC =AB,AE⊥BC,
∴CE= BE,
∴AM为BC的中垂线,
∴CM=BM
∵EM⊥BC,
∴EM平分∠CMB,(等腰三角形三线合一)
∴∠CME=∠BME.
∴∠BME= ∠PMF,∠PMF=∠CME,
∴∠MCD= ∠F(三角形内角和).


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:初中数学 来源: 题型:
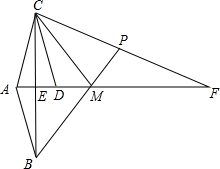 与线段CF,AF相交于P,M.
与线段CF,AF相交于P,M.查看答案和解析>>
科目:初中数学 来源: 题型:
 已知:如图,AF平分∠BAC,BC⊥AF于点E,点D在AF上,ED=EA,点P在CF上,连接PB交AF于点M.若∠BAC=2∠MPC,请你判断∠F与∠MCD的数量关系,并说明理由.
已知:如图,AF平分∠BAC,BC⊥AF于点E,点D在AF上,ED=EA,点P在CF上,连接PB交AF于点M.若∠BAC=2∠MPC,请你判断∠F与∠MCD的数量关系,并说明理由.查看答案和解析>>
科目:初中数学 来源:2010-2011学年湖北省宜昌市夷陵区鄢家河初中九年级(上)月考数学试卷(9月份)(解析版) 题型:解答题
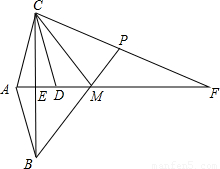
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com