
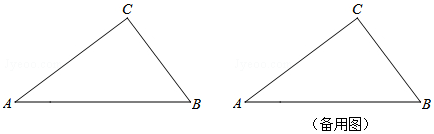
分析 (1)直接利用勾股定的逆定理得出△ABC是直角三角形;
(2)由于动点P从点C开始,按C→A→B的路径运动,故应分点P在AC上与AB上两种情况进行讨论;
(3)当P、Q两点之间的距离为$\sqrt{5}$时,分三种情况讨论:点P在AC上,点Q在BC上;点P、Q均在AB上运动,且点P在点Q的左侧;点P、Q均在AB上运动,且点P在点Q的右侧,分别求得t的值并检验即可.
解答 解:(1)△ABC是直角三角形.
∵AB=5,BC=3,AC=4,
∴AC2+BC2=25=AB2,
∴△ABC是直角三角形;
(2)如图,当点P在AC上时,CP=CB=3,则t=3÷2=1.5秒;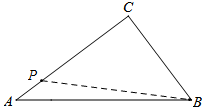
如图,当点P在AB上时,分两种情况: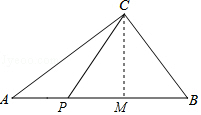
若BP=BC=3,则AP=2,
故t=(4+2)÷2=3秒;
若CP=CB=3,作CM⊥AB于M,则
$\frac{1}{2}$×AB×MC=$\frac{1}{2}$×BC×AC,
$\frac{1}{2}$×5×MC=$\frac{1}{2}$×3×4,
解得CM=2.4,
∴由勾股定理可得PM=BM=1.8,即BP=3.6,
∴AP=1.4,
故t=(4+1.4)÷2=2.7秒.
综上所述,当t=1.5、3或2.7 时,△BCP是以BC为腰的等腰三角形.
故答案为:t=1.5或2.7或3;
(3)①如图,当点P在AC上,点Q在BC上运动时(0≤t≤2),
由勾股定理可得:(2t)2+t2=5,
解得t=1;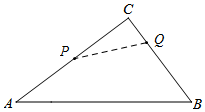
②如图,当点P、Q均在AB上运动,且点P在点Q的左侧时(3≤t<4),
由题可得:12-2t-t=$\sqrt{5}$,
解得t=$\frac{12-\sqrt{5}}{3}$;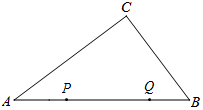
③当点P、Q均在AB上运动,且点P在点Q的右侧时(4<t≤4.5),
由题可得:2t+t-12=$\sqrt{5}$,
解得t=$\frac{12+\sqrt{5}}{3}$,
∵t=$\frac{12+\sqrt{5}}{3}$>4.5,
∴不成立,舍去.
综上所述,当t为1秒或$\frac{12-\sqrt{5}}{3}$秒时,P、Q两点之间的距离为$\sqrt{5}$.
点评 本题属于三角形综合题,主要考查了勾股定理及其逆定理的应用以及等腰三角形的判定与性质的运用,在解答此题时要注意进行分类讨论,不要漏解.


科目:初中数学 来源: 题型:解答题
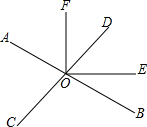 如图,两直线AB、CD相交于点O,OE平分∠BOD,如果∠AOC:∠AOD=7:11,
如图,两直线AB、CD相交于点O,OE平分∠BOD,如果∠AOC:∠AOD=7:11,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,CD是⊙O的直径,线段AB过圆心O,且OA=OB=$\sqrt{5}$,CD=2,连接AC、AD、BD、BC、AD、CB分别交⊙O于E、F.当AC与⊙O相切时,问四边形CEDF是何种特殊四边形?请证明你的结论.
如图,CD是⊙O的直径,线段AB过圆心O,且OA=OB=$\sqrt{5}$,CD=2,连接AC、AD、BD、BC、AD、CB分别交⊙O于E、F.当AC与⊙O相切时,问四边形CEDF是何种特殊四边形?请证明你的结论.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
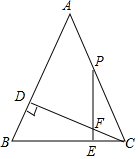 已知:在△ABC中,AB=AC,CD是AB边上的高,点P是AC边上任意一点(不与点A、点C重合)过点P作PE⊥BC,垂足为E,交CD于点F.若AD=CD,探究线段PF、CE之间的数量关系,并证明你的结论.
已知:在△ABC中,AB=AC,CD是AB边上的高,点P是AC边上任意一点(不与点A、点C重合)过点P作PE⊥BC,垂足为E,交CD于点F.若AD=CD,探究线段PF、CE之间的数量关系,并证明你的结论.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com