
如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于E.
(1)求证:点E是边BC的中点;
(2)求证:BC2=BD•BA;
(3)当以点O、D、E、C为顶点的四边形是正方形时,求证:△ABC是等腰直角三角形.

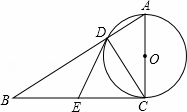
证明:(1)如图,连接OD.∵DE为切线,∴∠EDC+∠ODC=90°;
∵∠ACB=90°,∴∠ECD+∠OCD=90°.又∵OD=OC,∴∠ODC=∠OCD,
∴∠EDC=∠ECD,∴ED=EC;∵AC为直径,∴∠ADC=90°,
∴∠BDE+∠EDC=90°,∠B+∠ECD=90°,∴∠B=∠BDE,∴ED=DB.
∴EB=EC,即点E为边BC的中点;
(2)∵AC为直径,∴∠ADC=∠ACB=90°,又∵∠B=∠B
∴△ABC∽△CDB,∴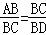 ,∴BC2=BD•BA;
,∴BC2=BD•BA;
(3)当四边形ODEC为正方形时,∠OCD=45°;∵AC为直径,
∴∠ADC=90°,∴∠CAD=∠ADC﹣∠OCD=90°﹣45°=45°
∴Rt△ABC为等腰直角三角形.


科目:初中数学 来源: 题型:
已知关于x的一元二次方程x2﹣2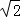 x+m=0,有两个不相等的实数根.
x+m=0,有两个不相等的实数根.
(1)求实数m的最大整数值;
(2)在(1)的条下,方程的实数根是x1,x2,求代数式x12+x22﹣x1x2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在Rt△ABC中,∠B=90°,分别以点A、C为圆心,大于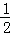 AC长为半径画弧,两弧相交于点M、N,连接MN,与AC、BC分别交于点D、E,连接AE.
AC长为半径画弧,两弧相交于点M、N,连接MN,与AC、BC分别交于点D、E,连接AE.
(1)求∠ADE;(直接写出结果)
(2)当AB=3,AC=5时,求△ABE的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
如图①,在平面直角坐标系中,点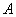 的坐标为(
的坐标为(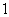 ,
,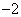 ),点
),点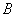 (3,
(3,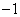 ),二次函数
),二次函数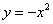 的图象为
的图象为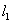 。
。
(1)平移抛物线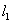 ,使平移后的抛物线经过点
,使平移后的抛物线经过点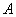 ,但不经过点
,但不经过点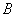 。
。
①满足此条件的函数解析式有 个;
②写出向下平移且过点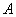 的解析式 。
的解析式 。
(2)平移抛物线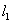 ,使平移后的抛物线经过
,使平移后的抛物线经过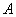 、
、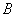 两点,所得的抛物线为
两点,所得的抛物线为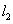 ,如图②,求抛物线
,如图②,求抛物线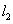 的解析式及顶点坐标,并求
的解析式及顶点坐标,并求 的面积;
的面积;
(3)在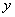 轴上是否存在点
轴上是否存在点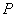 ,使
,使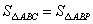 ,若存在,求出点
,若存在,求出点 的坐标;若不存在,请说明好理由。
的坐标;若不存在,请说明好理由。




查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com