练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    1．已知一直线与直线y=-$\frac{1}{3}$x平行，且经过点（0，-5），则这条直线解析式为y=-$\frac{1}{3}$x-5．

    分析 由平行关系确定直线解析式的一次项系数，再将点（0，-5）代入求解析式的常数项．

    解答 解：设所求直线解析式为y=kx+b，
    ∵所求直线平行于直线y=-$\frac{1}{3}$x，
    ∴k=-$\frac{1}{3}$，
    将（0，-5）代入y=-$\frac{1}{3}$x+b中，得b=-5，
    ∴所求直线解析式为y=-$\frac{1}{3}$x-5，
    故答案为：y=-$\frac{1}{3}$x-5．

    点评 本题考查的是待定系数法求一次函数解析式．关键是根据直线与直线的平行关系确定一次项系数．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    9．某校随机抽取了九年级的30名学生，测试了他们1分钟仰卧起坐的次数，并绘制如图所示的频数分布直方图，请根据图示计算，仰卧起坐次数在24.5～29.5之间的频率是（　　）
    A．0.1B．0.17C．0.33D．0.4

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．解方组$\left\{\begin{array}{l}{x-y=1}\\{{x}^{2}-\frac{{y}^{2}}{2}=1}\end{array}\right.$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    9．关于三角形的角平分线和中线，下列说法正确的是（　　）
    A．都是直线B．都是射线
    C．都是线段D．可以是射线也可以是线段

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    16．火车票上的车次号有两个意义，一是数字越小表示车速快，1～98次为特快列车，101～198次为直快列车，301～398次为普快列车，401～498次为普客列车；二是单数与双数表示不同的行驶方向，其中单数表示从北京开出，双数表示开往北京．根据以上规定，北京开往杭州的某一直快列车的车次号可能是（　　）
    A．20B．119C．120D．319

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．如图，已知CB⊥AB，点E在AB上，且CE平分∠BCD，DE平分∠ADC，∠EDC+∠DCE=90°，求证：DA⊥AB．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

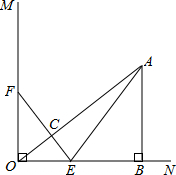    13．如图，已知∠MON=90°，A是∠MON内部的一点，过点A作AB⊥ON，垂足为点B，AB=3厘米，OB=4厘米，动点E，F同时从O点出发，点E以1.5厘米/秒的速度沿ON方向运动，点F以2厘米/秒的速度OM方向运动，EF与OA交于点C，连接AE，当点E到达点B时，点F随之停止运动．设运动时间为t秒（t＞0）
    （1）当t=1秒时，△EOF与△ABO是否相似？请说明理由；
    （2）在运动过程中，不论t取何值，总有EF⊥OA，为什么？
    （3）连接AF，在运动过程中，是否存在某一时刻t，使得S△AEF=$\frac{1}{2}$S四边形AEOF
    若存在，请求出此时t的值：若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．分解因式
    （1）x3-x
    （2）3m2n-12mn+12n．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

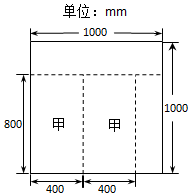    11．某装修公司为陶博会布置展厅，为了达到最佳装修效果，需用甲、乙两种型号的瓷砖．经计算，甲种型号瓷砖需用180块，乙种型号瓷砖需用120块，甲种型号瓷砖规格为800mm×400mm，乙种型号瓷砖规格为300mm×500mm，市场上只有同种花色的标准瓷砖，规格为1000mm×1000mm．一块标准瓷砖尽可能多的加工出甲、乙两种型号的瓷砖，公司共设计了三种加工方案（见下表）．（图①是方案二的加工示意图）
    方案一方案二方案三
    甲种型号瓷砖块数12b
    乙种型号瓷砖块数a06
    设购买的标准瓷砖全部加工完，其中按方案一加工x块，按方案二加工y块，按方案三加工z块，且加工好的甲、乙两种型号瓷砖刚好够用．
    （1）表中a=4，b=0；
    （2）分别求出y与x，z与x之间的函数关系式；
    （3）若用W表示所购标准瓷砖的块数，求W与x的函数关系式，并指出当x取何值时W最小，此时按三种加工方案各加工多少块标准瓷砖？

    查看答案和解析>>

    同步练习册答案