
【题目】已知:![]() 关于
关于![]() 的函数
的函数![]() 的图象与坐标轴只有两个不同的交点
的图象与坐标轴只有两个不同的交点![]() 、
、![]() ,
,![]() 点坐标为
点坐标为![]() ,则
,则![]() 的面积为_____.
的面积为_____.
【答案】1或![]()
【解析】
根据k是否为0分类讨论,当k=0时,求出点B和点A的坐标,利用待定系数法求出直线AP的解析式,即可求出AP与y轴交点C的坐标,然后根据S△PAB=S△ABC+S△PBC即可求出结论;当k≠0时,根据题意可知抛物线与x轴只有一个交点,从而求出k的值,然后求出点B和点A的坐标,利用待定系数法求出直线AP的解析式,即可求出AP与y轴交点C的坐标,然后根据S△PAB=S△ABC+S△PBC即可求出结论.
解:当k=0时,![]()
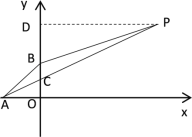
设![]() 与x轴交于点A,与y轴交于点B,AP与y轴交于点C,则点A(-1,0),点B(0,1),过点P作PD⊥y轴于D,则PD=3,OA=1
与x轴交于点A,与y轴交于点B,AP与y轴交于点C,则点A(-1,0),点B(0,1),过点P作PD⊥y轴于D,则PD=3,OA=1
设直线AP的解析式为y=ax+b
将点A和点P的坐标代入,得
![]()
解得:![]()
∴直线AP的解析式为![]()
将x=0代入,解得y=![]()
∴点C的坐标为(0,![]() )
)
∴BC=1-![]() =
=![]()
∴S△PAB=S△ABC+S△PBC=![]() BC·OA+
BC·OA+![]() BC·PD=
BC·PD=![]() ×
×![]() ×1+
×1+![]() ×
×![]() ×3=1;
×3=1;
当k≠0时,![]() 是
是![]() 的二次函数,图象必与y轴交于一点B(0,1)
的二次函数,图象必与y轴交于一点B(0,1)
∵![]() 的图象与坐标轴只有两个不同的交点
的图象与坐标轴只有两个不同的交点![]() 、
、![]() ,
,
∴![]()
解得:![]()
∴二次函数解析式为![]()
将y=0代入,得![]()
解得:x1=x2=-4
∴点A的坐标为(-4,0),即AO=4
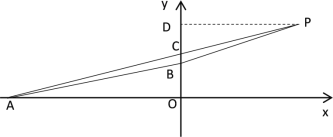
设直线AP的解析式为y=ax+b
将点A和点P的坐标代入,得
![]()
解得:![]()
∴直线AP的解析式为![]()
将x=0代入,解得y=![]()
∴点C的坐标为(0,![]() )
)
∴BC=![]() -1=
-1=![]()
∴S△PAB=S△ABC+S△PBC=![]() BC·OA+
BC·OA+![]() BC·PD=
BC·PD=![]() ×
×![]() ×4+
×4+![]() ×
×![]() ×3=
×3=![]() ;
;
综上:S△PAB=1或![]()
故答案为:1或![]() .
.


科目:初中数学 来源: 题型:
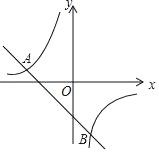
【题目】如图,一次函数y1=kx+b(k≠0)和反比例函数![]() 的图象相交于点A(﹣4,2),B(n,﹣4)
的图象相交于点A(﹣4,2),B(n,﹣4)
(1)求一次函数和反比例函数的表达式;
(2)观察图象,直接写出不等式y1<y2的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知抛物线![]() 的顶点为
的顶点为![]() ,与
,与![]() 轴的交点为
轴的交点为![]() ,
,![]() .
.

(1)求抛物线的解析式;
(2)M为![]() 轴上方抛物线上的一点,
轴上方抛物线上的一点,![]() 与抛物线的对称轴交于点
与抛物线的对称轴交于点![]() ,若
,若![]() ,求点
,求点![]() 的坐标;
的坐标;
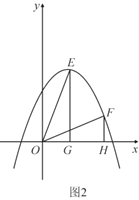
(3)如图2,将原抛物线沿对称轴平移后得到新抛物线为![]() ,
,![]() ,
,![]() 是新抛物线在第一象限内互不重合的两点,
是新抛物线在第一象限内互不重合的两点,![]() 轴,
轴,![]() 轴,垂足分别为
轴,垂足分别为![]() ,
,![]() ,若始终存在这样的点
,若始终存在这样的点![]() ,
,![]() ,满足
,满足![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
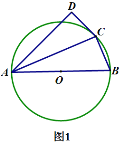
【题目】如图1,![]() 是
是![]() 的外接,
的外接,![]() 是直径,
是直径,![]() 是
是![]() 外一点且满足
外一点且满足![]() ,连接
,连接![]() .
.
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() ,
,![]() ,
,![]() ,求直径
,求直径![]() 的长;
的长;
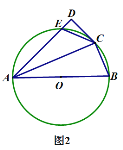
(3)如图2,当![]() 时,
时,![]() 与
与![]() 交于
交于![]() 点,试写出
点,试写出![]() 、
、![]() 、
、![]() 之间的数量关系并证明.
之间的数量关系并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知Rt△EBC中,∠B=90°,A为BE边上一点,以边AC上的点O为圆心、OA为半径的圆O与EC相切,D为切点,AD∥BC.
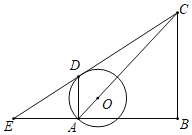
(1)求证:∠E=∠ACB.
(2)若AD=1,![]() ,求BC的长.
,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
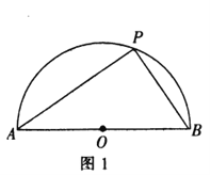
【题目】[问题发现]如图1,半圆![]() 的直径
的直径![]() 是半圆
是半圆![]() 上的一个动点,则
上的一个动点,则![]() 面积的最大值是_.
面积的最大值是_.
[问题解决]如图2所示的是某街心花园的一角.在扇形![]() 中,
中,![]() 米,在围墙
米,在围墙![]() 和
和![]() 上分别有两个入口
上分别有两个入口![]() 和
和![]() 且
且![]() 米,
米,![]() 是
是![]() 的中点,出口
的中点,出口![]() 在
在![]() 上.现准备沿
上.现准备沿![]() 从入口到出口铺设两条景观小路,在四边形
从入口到出口铺设两条景观小路,在四边形![]() 内种花,在剩余区域种草.
内种花,在剩余区域种草.
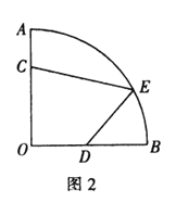
①出口![]() 设在距直线
设在距直线![]() 多远处可以使四边形
多远处可以使四边形![]() 的面积最大?最大面积是多少?(小路宽度不计)
的面积最大?最大面积是多少?(小路宽度不计)
②已知铺设小路![]() 所用的普通石材每米的造价是
所用的普通石材每米的造价是![]() 元,铺设小路
元,铺设小路![]() 所用的景观石材每米的造价是
所用的景观石材每米的造价是![]() 元问:在
元问:在![]() 上是否存在点
上是否存在点![]() ,使铺设小路
,使铺设小路![]() 和
和![]() 的总造价最低?若存在,请求出最低总造价和出口
的总造价最低?若存在,请求出最低总造价和出口![]() 距直线
距直线![]() 的距离;若不存在,请说明理由.
的距离;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读以下材料,并按要求完成相应的任务:
莱昂哈德·欧拉(Leonhard Euler)是瑞士数学家,在数学上经常见到以他的名字命名的重要常数、公式和定理,下面是欧拉发现的一个定理:在△ABC 中,R 和 r 分别为外接圆和内切圆的半径,O 和 I 分别为其外心和内心,则OI ![]() R
R![]() 2Rr .
2Rr .
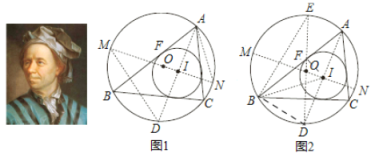
下面是该定理的证明过程(借助了第(2)问的结论):
延长AI 交⊙O 于点 D,过点 I 作⊙O 的直径 MN,连接 DM,AN.
∵∠D=∠N,∴∠DMI=∠NAI(同弧所对的圆周角相等),
∴△MDI∽△ANI.∴![]() ,∴ IA ID IM IN ①
,∴ IA ID IM IN ①
如图②,在图 1(隐去 MD,AN)的基础上作⊙O 的直径DE,连接BE,BD,BI,IF
∵DE 是⊙O 的直径,∴∠DBE=90°.
∵⊙I 与 AB 相切于点 F,∴∠AFI=90°,
∴∠DBE=∠IFA.
∵∠BAD=∠E(同弧所对圆周角相等),
∴△AIF∽△EDB.
∴![]() ,∴
,∴![]() ②,
②,
由(2)知:![]() ,
,
∴![]()
又∵![]() ,
,
∴ 2Rr(R d )(R d ) ,
∴ R![]() d
d![]() 2Rr
2Rr
∴ d ![]() R
R![]() 2Rr
2Rr
任务:(1)观察发现: IM R d , IN (用含R,d 的代数式表示);
(2)请判断 BD 和 ID 的数量关系,并说明理由.(请利用图 1 证明)
(3)应用:若△ABC 的外接圆的半径为 6cm,内切圆的半径为 2cm,则△ABC 的外心与内心之间的距离为 cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:抛物线y=a(x2﹣2mx﹣3m2)(m0)交x轴于A、B两点(其中A点在B点左侧),交y轴于点C.
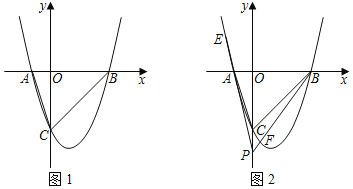
(1)若A点坐标为(﹣1,0),则B点坐标为 .
(2)如图1,在 (1)的条件下,且am=1,设点M在y轴上且满足∠OCA+∠AMO=∠ABC,试求点M坐标.
(3)如图2,在y轴上有一点P(0,n)(点P在点C的下方),直线PA、PB分别交抛物线于点E、F,若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com