
 下面是小东的探究学习过程,请补充完整:
下面是小东的探究学习过程,请补充完整:| x | … | -3 | -2 | -1 | -$\frac{1}{2}$ | 0 | $\frac{1}{5}$ | $\frac{1}{2}$ | $\frac{4}{5}$ | … |
| y | … | -$\frac{1}{8}$ | $\frac{1}{3}$ | $\frac{3}{4}$ | $\frac{11}{12}$ | 1 | $\frac{39}{40}$ | m | -$\frac{3}{5}$ | … |
分析 (1)①当x=$\frac{1}{2}$时,y=$\frac{3}{4}$,则m=$\frac{3}{4}$.②利用描点法即可画出函数的图象.③根据函数的图象,即可解决问题.
(2)结合函数的图象,即可解决问题.
解答 解:(1)①当x=$\frac{1}{2}$时,y=$\frac{3}{4}$.
∴$m=\frac{3}{4}$.
②该函数的图象如下图所示: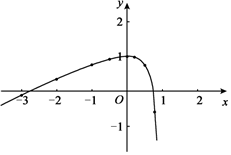
③答案不惟一,如:当x<0时,y随x的增大而增大.
(2)答案不惟一,如:函数图象的最高点坐标为(1,2).
点评 本题考查函数的图象与性质没解题的关键是理解题意,学会利用描点法画出函数图象,学会利用函数的图象解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
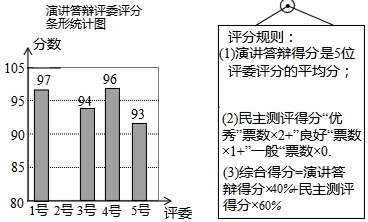
| 票数 | |
| 优秀 | 40 |
| 良好 | 5 |
| 一般 | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com