
【题目】如图,在△ABC中,以AB为直径的⊙O分别于BC,AC相交于点D,E,BD=CD,过点D作⊙O的切线交边AC于点F.
(1)求证:DF⊥AC;
(2)若⊙O的半径为5,∠CDF=30°,求![]() 的长(结果保留π).
的长(结果保留π).

【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)连接OD,由切线的性质即可得出∠ODF=90°,再由BD=CD,OA=OB可得出OD是△ABC的中位线,根据三角形中位线的性质即可得出,根据平行线的性质即可得出∠CFD=∠ODF=90°,从而证出DF⊥AC;
(2)由∠CDF=30°以及∠ODF=90°即可算出∠ODB=60°,再结合OB=OD可得出△OBD是等边三角形,根据弧长公式即可得出结论.
试题解析:(1)证明:连接OD,如图所示.∵DF是⊙O的切线,D为切点,∴OD⊥DF,∴∠ODF=90°.
∵BD=CD,OA=OB,∴OD是△ABC的中位线,∴OD∥AC,∴∠CFD=∠ODF=90°,∴DF⊥AC.
(2)解:∵∠CDF=30°,由(1)得∠ODF=90°,∴∠ODB=180°﹣∠CDF﹣∠ODF=60°.∵OB=OD,∴△OBD是等边三角形,∴∠BOD=60°,∴![]() 的长=
的长=![]() =
=![]() =
=![]() .
.



 天天向上口算本系列答案
天天向上口算本系列答案科目:初中数学 来源: 题型:
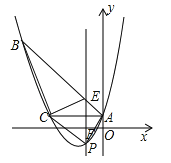
【题目】如图,已知抛物线![]() 经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P是直线AC下方抛物线上的动点.
经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P是直线AC下方抛物线上的动点.
(1)求抛物线的解析式;
(2)过点P且与y轴平行的直线l与直线AB、AC分别交于点E、F,当四边形AECP的面积最大时,求点P的坐标;
(3)当点P为抛物线的顶点时,在直线AC上是否存在点Q,使得以C、P、Q为顶点的三角形与△ABC相似,若存在,求出点Q的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8,在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,则D点的坐标是 . 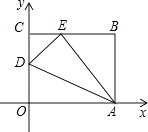
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系XOY中,A(﹣1,5),B(﹣1,0),C(﹣4,3). 
(1)请画出△ABC关于y轴对称的△A′B′C′(其中A′,B′,C′分别是A,B,C的对应点,不写画法);
(2)直接写出A′,B′,C′三点的坐标:A′( ),B′( ),C′( )
(3)计算△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂生产A,B两种产品,其单价随市场变化而做相应调整.营销人员根据前三次单价变化的情况,绘制了单价变化不完整的统计表及折线图.
A,B产品单价变化统计表
第一次 | 第二次 | 第三次 | |
A产品单价(元/件) | 6 | 5.2 | 6.5 |
B产品单价(元/件) | 3.5 | 4 | 3 |
并求得了A产品三次单价的平均数和方差:![]() =5.9,SA2=
=5.9,SA2= ![]() [(6﹣5.9)2+(5.2﹣5.9)2+(6.5﹣5.9)2]=
[(6﹣5.9)2+(5.2﹣5.9)2+(6.5﹣5.9)2]= ![]()
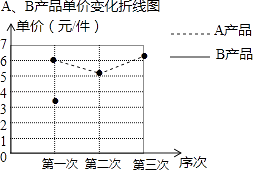
(1)在折线图中画出B产品的单价变化的情况;
(2)求B产品三次单价的方差;
(3)该厂决定第四次调价,A产品的单价仍为6.5元/件,B产品的单价比3元/件的基础上调m%(m>0),但调价后不能超过4元/件,并且使得A产品这四次单价的中位数是B产品四次单价中位数的2倍少1,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC在平面直角坐标系中,点A、B、C都在第一象限内,现将△ABC的三个顶点的横坐标保持不变,纵坐标都乘-1,得到一个新的三角形,则( )。
A. 新三角形与△ABC关于x轴对称 B. 新三角形与△ABC关于y轴对称
C. 新三角形的三个顶点都在第三象限内 D. 新三角形是由△ABC沿y轴向下平移一个单位长度得到的
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的对角线AC与BD相交于点O,∠ACB的角平分线分别交AB,BD于M,N两点.若AM=2,则线段ON的长为( ) 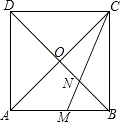
A.![]()
B.![]()
C.1
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com