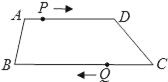
【题目】已知：如图，在梯形ABCD中，AD∥BC，AD＝24cm，BC＝30cm，点P自点A向D以1cm/s的速度运动，到D点即停止．点Q自点C向B以2cm/s的速度运动，到B点即停止，直线PQ截梯形为两个四边形．问当P，Q同时出发，几秒时其中一个四边形为平行四边形？
【答案】当8秒或10秒时，其中一个四边形是平行四边形.
【解析】试题分析：若四边形PDCQ或四边形APQB是平行四边形，那么QD=CQ或AP=BQ或PD=BQ，根据这个结论列出方程就可以求出时间．
试题解析：设P，Q同时出发t秒后四边形PDCQ或四边形APQB是平行四边形，根据已知得到AP=t，PD=24t，CQ=2t，BQ=302t.
(1)若四边形PDCQ是平行四边形，则PD=CQ，
∴24t=2t，
∴t=8，
∴8秒后四边形PDCQ是平行四边形；
(2)若四边形APQB是平行四边形，则AP=BQ，
∴t=302t，
∴t=10，
∴10秒后四边形APQB是平行四边形.
∴出发后8秒或10秒其中一个是平行四边形.
科目：初中数学 来源： 题型：
【题目】某种商品的标价为500元/件，经过两次降价后的价格为320元/件，并且两次降价的百分率相同.
（1）求该种商品每次降价的百分率；
（2）若该商品进价为280元/件，两次降价共售此种商品100件，为使两次降价销售的总利润不少于8000元，则第一次降价后至少要售出这种商品多少件？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】探索n×n的正方形钉子板上(n是钉子板每边上的钉子数,每边上相邻钉子间的距离为1),连接任意两个钉子所得到的不同长度值的线段种数:
当n=2时,钉子板上所连不同线段的长度值只有1与
，所以不同长度值的线段只有2种,若用S表示不同长度值的线段种数,则S=2;
当n=3时,钉子板上所连不同线段的长度值只有1, 
，2, 
，2
五种,比n=2时增加了3种,即S=2+3=5.
(1)观察图形,填写下表:
钉子数(n×n) | S值 |
2×2 | 2 |
3×3 | 2+3 |
4×4 | 2+3+（____） |
5×5 | （________） |
(2)写出(n-1)×(n-1)和n×n的两个钉子板上,不同长度值的线段种数之间的关系;(用式子或语言表述均可).
(3)对n×n的钉子板,写出用n表示S的代数式.
查看答案和解析>>
科目：初中数学 来源： 题型：
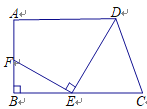
【题目】如图，在梯形ABCD中，已知AD∥BC，∠B=90°，AB=7，AD=9，BC=12，在线段BC上任取一点E，连接DE，作EF⊥DE，交直线AB于点F.
（1）若点F与B重合，求CE的长；（3分）
（2）若点F在线段AB上，且AF=CE，求CE的长.（5分）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某片果园有果树80棵，现准备多种一些果树提高果园产量，但是如果多种树，那么树之间的距离和每棵树所受光照就会减少，单棵树的产量随之降低，若该果园每棵果树产果y千克，增种果树x棵，它们之间的函数关系如图所示．
(1)求y与x之间的函数解析式；
(2)在投入成本最低的情况下，增种果树多少棵时，果园可以收获果实6750千克？
(3)当增种果树多少棵时，果园的总产量w（千克）最大？最大产量是多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
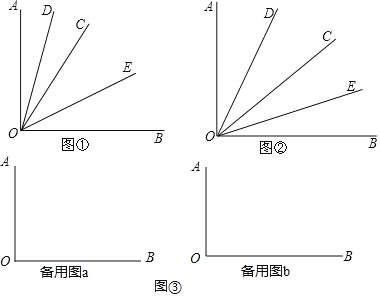
【题目】已知：∠AOB是一个直角，作射线OC，再分别作∠AOC和∠BOC的平分线OD、OE．
（1）如图①，当∠BOC=70°时，求∠DOE的度数；
（2）如图②，若射线OC在∠AOB内部绕O点旋转，当∠BOC=α时，求∠DOE的度数.
（3）如图③，当射线OC在∠AOB外绕O点旋转时，画出图形，直接写出∠DOE的度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
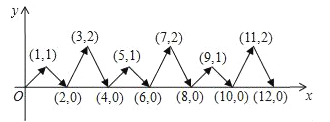
【题目】如图，动点P在平面直角坐标系中按图中箭头所示方向运动，第1次从顶点运动到点（1，1），第2次接着运动到点（2，0），第3次接着运动到点（3，2），…按这样的运动规律，经过第2010次运动后，动点P的坐标是_____．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
