
科目:初中数学 来源:2017-2018学年九年级数学北师大版上册 第3章 概率的进一步认识 单元测试卷 题型:解答题
经过某十字路口的汽车,它可能继续直行,也可能向左转或向右转,如果这三种情况是等可能的,当三辆汽车经过这个十字路口时:
(1)求三辆车全部同向而行的概率;
(2)求至少有两辆车向左转的概率.
(1)(2) 【解析】试题分析:因为此题需要三步完成,所以画出树状图求解即可,注意要做到不重不漏. 试题解析:(1)画树状图如下: 总共有27种结果,每种结果出现的可能性相同.其中,三辆车全部同向而行的结果有3种,(7分)∴P(三辆车全部同向而行)=; (2)由(1)中树状图可知至少有两辆车向左转的结果有7种, ∴P(至少有两辆车向左转)=.查看答案和解析>>
科目:初中数学 来源:2017-2018学年八年级数学人教版上册 全册综合测试卷 题型:单选题
如图,点B、F、C、E在一条直线上,AB∥ED,AC∥FD,那么添加下列一个条件后,仍无法判定△ABC≌△DEF的是( )

A. AB=DE B. AC=DF C. ∠A=∠D D. BF=EC
C 【解析】试题分析:【解析】 选项A、添加AB=DE可用AAS进行判定,故本选项错误; 选项B、添加AC=DF可用AAS进行判定,故本选项错误; 选项C、添加∠A=∠D不能判定△ABC≌△DEF,故本选项正确; 选项D、添加BF=EC可得出BC=EF,然后可用ASA进行判定,故本选项错误. 故选C.查看答案和解析>>
科目:初中数学 来源:湖南邵阳市区2017-2018学年八年级上册数学期末试卷 题型:填空题
如图,∠ACB=90°,AC=BC,BE⊥CE,AD⊥CE于D,AD=2cm,BE=0.5cm,则DE=________cm.

查看答案和解析>>
科目:初中数学 来源:湖南邵阳市区2017-2018学年八年级上册数学期末试卷 题型:单选题
甲、乙两人同时从A地出发,骑自行车行30千米到B地,甲比乙每小时少走3千米,结果乙先到40分钟。若设乙每小时走x千米,则可列方程( )
A.  B.
B. 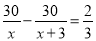 C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源:2018人教版八年级数学下册练习:第十七章达标检测卷 题型:解答题
如图,将长方形OABC置于平面直角坐标系中,点A的坐标为(0,4),点C的坐标为(m,0)(m>0),点D(m,1)在BC上,将长方形OABC沿AD折叠压平,使点B落在坐标平面内,设点B的对应点为点E.
(1)当m=3时,点B的坐标为_________,点E的坐标为_________;
(2)随着m的变化,试探索:点E能否恰好落在x轴上?若能,请求出m的值;若不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源:2018人教版八年级数学下册练习:第十七章达标检测卷 题型:填空题
如图,从点A(0,2)发出一束光,经x轴反射,过点B(4,3),则这束光从点A到点B所经过的路径的长为_____.

查看答案和解析>>
科目:初中数学 来源:湖北省襄阳老河口市2018届九年级上学期期末考试数学试卷 题型:解答题
一名男生推铅球,铅球行进的高度y(单位:m)与水平距离x(单位:m)之间的关系是 .
.
(1)铅球行进的最大高度是多少?
(2)该男生把铅球推出的水平距离是多少?
(3)铅球在下落的过程中,行进高度由 m变为
m变为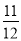 m时,铅球行进的水平距离是多少?
m时,铅球行进的水平距离是多少?
查看答案和解析>>
科目:初中数学 来源:2017-2018学年北师大版七年级数学上册:第5章 一元一次方程 单元测试卷 题型:单选题
如图,在长方形ABCD中,AB=10cm,BC=6cm,动点P,Q分别从点A,B同时出发,点P以3cm/s的速度沿AB,BC向点C运动,点Q以1cm/s的速度沿BC向点C运动.设P,Q运动的时间是t秒,当点P与点Q重合时t的值是( )

A.  B. 4 C. 5 D. 6
B. 4 C. 5 D. 6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com