
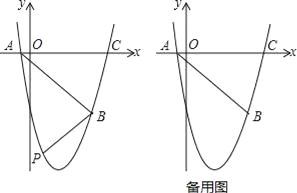
【题目】如图,抛物线y=ax2+bx+c(a≠0)经过点 经过点A(﹣1,0),B(5,﹣6),C(6,0)
(1)求抛物线的解析式;
(2)如图,在直线AB下方的抛物线上是否存在点P使四边形PACB的面积最大?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)若点Q为抛物线的对称轴上的一个动点,试指出△QAB为等腰三角形的点Q一共有几个?并请求出其中某一个点Q的坐标.
【答案】(1)y=x2﹣5x﹣6;(2)存在,P(2,﹣12);(3)Q点一共有5个,(![]() ,﹣
,﹣![]() ).
).
【解析】试题分析:(1)抛物线经过点A(﹣1,0),B(5,﹣6),C(6,0),可利用两点式法设抛物线的解析式为y=a(x+1)(x﹣6),代入B(5,﹣6)即可求得函数的解析式;(2)作辅助线,将四边形PACB分成三个图形,两个三角形和一个梯形,设P(m,m2﹣5m﹣6),四边形PACB的面积为S,用字母m表示出四边形PACB的面积S,发现是一个二次函数,利用顶点坐标求极值,从而求出点P的坐标.(3)分三种情况画图:①以A为圆心,AB为半径画弧,交对称轴于Q1和Q4,有两个符合条件的Q1和Q4;②以B为圆心,以BA为半径画弧,也有两个符合条件的Q2和Q5;③作AB的垂直平分线交对称轴于一点Q3,有一个符合条件的Q3;最后利用等腰三角形的腰相等,利用勾股定理列方程求出Q3坐标.
试题解析:(1)设y=a(x+1)(x﹣6)(a≠0),
把B(5,﹣6)代入:a(5+1)(5﹣6)=﹣6,
a=1,
∴y=(x+1)(x﹣6)=x2﹣5x﹣6;
(2)存在,
如图1,分别过P、B向x轴作垂线PM和BN,垂足分别为M、N,
设P(m,m2﹣5m﹣6),四边形PACB的面积为S,
则PM=﹣m2+5m+6,AM=m+1,MN=5﹣m,CN=6﹣5=1,BN=5,
∴S=S△AMP+S梯形PMNB+S△BNC
=![]() (﹣m2+5m+6)(m+1)+
(﹣m2+5m+6)(m+1)+![]() (6﹣m2+5m+6)(5﹣m)+
(6﹣m2+5m+6)(5﹣m)+![]() ×1×6
×1×6
=﹣3m2+12m+36
=﹣3(m﹣2)2+48,
当m=2时,S有最大值为48,这时m2﹣5m﹣6=22﹣5×2﹣6=﹣12,
∴P(2,﹣12),
(3)这样的Q点一共有5个,连接Q3A、Q3B,
y=x2﹣5x﹣6=(x﹣![]() )2﹣
)2﹣![]() ;
;
因为Q3在对称轴上,所以设Q3(![]() ,y),
,y),
∵△Q3AB是等腰三角形,且Q3A=Q3B,
由勾股定理得:(![]() +1)2+y2=(
+1)2+y2=(![]() ﹣5)2+(y+6)2,
﹣5)2+(y+6)2,
y=﹣![]() ,
,
∴Q3(![]() ,﹣
,﹣![]() ).
).



科目:初中数学 来源: 题型:
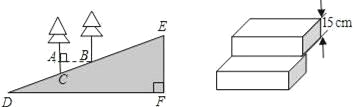
【题目】在徒骇河观景堤坝上有一段斜坡,为了方便游客通行,现准备铺上台阶,某施工队测得斜坡上铅锤的两棵树间水平距离AB=4米,斜坡距离BC=4.25米,斜坡总长DE=85米.
(1)求坡角∠D的度数(结果精确到1°)
(2)若这段斜坡用厚度为15cm的长方体台阶来铺,需要铺几级台阶?(最后一个高不足15cm时,按一个台阶计算)
(参考数据:cos20°≈0.94,sin20°≈0.34,sin18°≈0.31,cos18°≈0.95)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】给出一种运算:对于函数y=xn,规定y'=n×xn﹣1.若函数y=x4,则有y'=4×x3,已知函数y=x3,则方程y'=6x的解是( )
A. x=2B. x=3C. x1=0,x2=2D. x=﹣2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近似数4.50所表示的准确值a的取值范围是( )
A.4.495≤a<4.505
B.4040≤a<4.60
C.4.495≤a≤4.505
D.4.500≤a<4.5056
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】振子从一点A开始左右来回振动8次,如果规定向右为正,向左为负,这8次振动记录为(单位:毫米):+10,﹣9,+8,﹣6,+7.5,﹣6,+8,﹣7.
(1)求振子停止时所在位置距A点有多远?
(2)如果每毫米需时间0.02秒,则共用时间多少秒?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】眉山市三苏雕像广场是为了纪念三苏父子而修建的.原是一块长为(4a+2b)米,宽为(3a﹣b)米的长方形地块,现在政府对广场进行改造,计划将如图四周阴影部分进行绿化,中间将保留边长为(a+b)米的正方形三苏父子雕像,则绿化的面积是多少平方米?并求出当a=20,b=10时的绿化面积.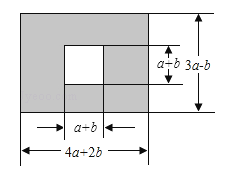
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形ABCD中,AD∥BC,分别添加下列条件之一:①AB∥CD;②AB=CD;③∠A=∠C;④∠B=∠C.能使四边形ABCD为平行四边形的条件的序号是____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com