
分析 (1)首先根据题意作图,由直角三角形两锐角互余,即可求得底角的度数,由等腰三角形的性质与三角形内角和定理即可求得顶角的度数;
(2)分别从△ABC是锐角三角形与钝角三角形去分析求解即可求得答案.
解答 解:(1)如图1: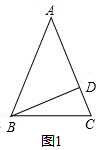
∵BD是△ABC的高,
∴BD⊥AC,
∴∠BDC=90°,
∵∠DBC=30°,
∴∠C=90°-∠DBC=60°,
∵AB=AC,
∴∠ABC=∠C=60°,
∴∠A=180°-∠ABC-∠C=60°,
故答案为:60°;
(2)如图2,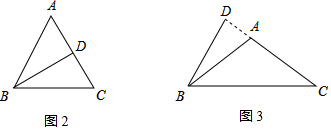
∵AB=AC,BD⊥AC,
∴∠ADB=90°,
∵∠ABD=30°,
∴∠A=60°;
如图3,
∵AB=AC,BD⊥AC,
∴∠BDC=90°,
∵∠ABD=30°,
∴∠BAD=60°,
∴∠BAC=120°;
综上所述,它的顶角度数为:60°或120°,
故答案为:60°或120°.
点评 此题考查了等腰三角形的性质.注意掌握分类讨论思想的应用是解此题的关键.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
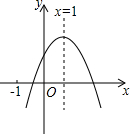 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc<0②b<a+c③4a+2b+c>0④2c<3b⑤a+b>m(am+b)(m≠1的实数),其中正确的结论的有( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc<0②b<a+c③4a+2b+c>0④2c<3b⑤a+b>m(am+b)(m≠1的实数),其中正确的结论的有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{25}{14}$ | B. | -$\frac{25}{14}$ | C. | $\frac{1}{14}$ | D. | -$\frac{1}{14}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
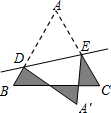 等腰△ABC的腰为6,底为5,D、E分别是AB、AC上的点,将△ADE沿直线DE折叠,点A落在点A′处,且点A′在△ABC外部,求阴影部分图形的周长.
等腰△ABC的腰为6,底为5,D、E分别是AB、AC上的点,将△ADE沿直线DE折叠,点A落在点A′处,且点A′在△ABC外部,求阴影部分图形的周长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com