
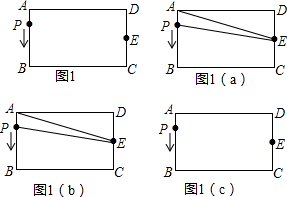
分析 (1)利用三角形面积求法S△APE=$\frac{1}{2}$AP•PE,即可解答;
(2)利用三角形面积求法S△APE=S梯形ABCE-S△ABP-S△PCE,分别得出答案;
(3)利用当0≤x≤4时,当4<x≤10时,当10<x≤12时,分别得出y与x的函数关系式即可;
解答 解:(1)如图1(a),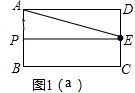
当x=2时,P为AB的中点,
∴△APE为直角三角形,PE=BC=6,
y=$\frac{1}{2}$×2×6=6.
(2)如图1(b),
当x=5时,则BP=1,
y=S△APE=S梯形ABCE-S△ABP-S△PCE
=$\frac{1}{2}$(AB+EC)×BC-$\frac{1}{2}$×AB×BP-$\frac{1}{2}$PC×EC
=$\frac{1}{2}$(4+2)×6-$\frac{1}{2}$×1×4-$\frac{1}{2}$×5×2
=11;
(3)如图1(c),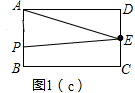
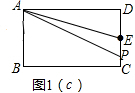
当0≤x≤4时,y=$\frac{1}{2}$x×6=3x;
当4<x≤10时,P在BC上,
y=S梯形ABCE-S△ABP′-S△P′CE
=18-$\frac{1}{2}$×4×(x-4)-$\frac{1}{2}$(10-x)×2
=16-x;
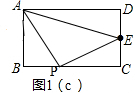
当10<x≤12时,P在EC上,
y=$\frac{1}{2}$×6×(12-x)=36-3x
综上所述:y=$\left\{\begin{array}{l}{3x(0≤x≤4)}\\{16-x(4<x≤10)}\\{36-3x(10<x≤12)}\end{array}\right.$.
点评 此题主要考查了三角形面积求法,利用分类讨论的思想求出y与x的函数关系式是解题关键.


 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案科目:初中数学 来源: 题型:解答题
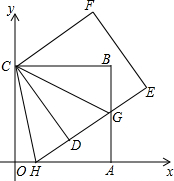 如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标为(6,6),将正方形ABCO绕点C逆时针旋转角度α(0°<α<90°),得到正方形CDEF,ED交线段AB于点G,ED的延长线交线段OA于点H,连结CH、CG.
如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标为(6,6),将正方形ABCO绕点C逆时针旋转角度α(0°<α<90°),得到正方形CDEF,ED交线段AB于点G,ED的延长线交线段OA于点H,连结CH、CG.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,直线y=2x+2交y轴于A点,交x轴于C点,以O,A,C为顶点作矩形OABC,将矩形OABC绕O点顺时针旋转90°,得到矩形ODEF,直线AC交直线DF于G点.
如图,直线y=2x+2交y轴于A点,交x轴于C点,以O,A,C为顶点作矩形OABC,将矩形OABC绕O点顺时针旋转90°,得到矩形ODEF,直线AC交直线DF于G点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
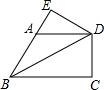 如图,在四边形ABCD中,∠ABC=60°,∠BAD=120°,∠ADC=90°,对角线BD平分∠ABC,过点D作DE⊥BA,交BA的延长线于点E.若AD=2,则四边形BCDE的周长为( )
如图,在四边形ABCD中,∠ABC=60°,∠BAD=120°,∠ADC=90°,对角线BD平分∠ABC,过点D作DE⊥BA,交BA的延长线于点E.若AD=2,则四边形BCDE的周长为( )| A. | 6+$\sqrt{3}$ | B. | 6+2$\sqrt{3}$ | C. | 7+$\sqrt{3}$ | D. | 7+2$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
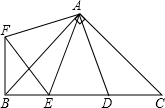 如图,在Rt△ABC中,AB=AC,D、E是斜边BC上两点,且∠DAE=45°,将△ADC绕点A顺时针旋转90°后,得到△AFB,连接EF,下列结论:①△AED≌△AEF;②△ABC的面积等于四边形AFBD的面积;③BE2+DC2=DE2;④BE+DC=DE,其中正确的是①②③(只填序号)
如图,在Rt△ABC中,AB=AC,D、E是斜边BC上两点,且∠DAE=45°,将△ADC绕点A顺时针旋转90°后,得到△AFB,连接EF,下列结论:①△AED≌△AEF;②△ABC的面积等于四边形AFBD的面积;③BE2+DC2=DE2;④BE+DC=DE,其中正确的是①②③(只填序号)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在正方形ABCD中,边长为2的等边△AEF的顶点E、F分别在BC和CD上,下列结论:
如图,在正方形ABCD中,边长为2的等边△AEF的顶点E、F分别在BC和CD上,下列结论:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com