
【题目】某中学开展“英语演讲”比赛活动,八年级(1),(2)班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如图所示,
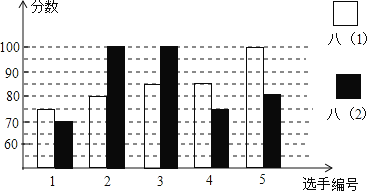
(1)根据图示填写下表:
班级 | 平均数(分) | 中位数(分) | 众数(分) |
八(1) | ______ | 85 | ______ |
八(2) | 85 | ______ | 100 |
(2)计算两班复赛成绩的方差并说明哪版的成绩比较稳定.(方差公式:S2=![]() ])
])
【答案】(1)85;85;80(2)八(1)班比八(2)班成绩更平稳一些.理由见解析
【解析】
(1)观察图分别写出八(1)班和八(2)班5名选手的复赛成绩,然后根据中位数的定义和平均数的求法以及众数的定义求解即可;
(2)先根据方差公式分别计算两个班复赛成绩的方差,再根据方差的意义判断即可.
解:(1)由图可知八(1)班5名选手的复赛成绩为:75、80、85、85、100,八(2)班5名选手的复赛成绩为:70、100、100、75、80,
所以八(1)的平均数为(70+100+100+75+80)÷5=85,八(1)的众数为85,
所以八(2)班的中位数是80;
填表如下:
班级 | 平均数(分) | 中位数(分) | 众数(分) |
八(1) | 85 | 85 | 85 |
八(2) | 85 | 80 | 100 |
故答案为:85,85,100;
(2)八(1)班比八(2)班成绩更平稳一些.理由如下:
S21班=![]() (75-85)2+(80-85)2+(85-85)2+(85-85)2+(100-85)2]=70,
(75-85)2+(80-85)2+(85-85)2+(85-85)2+(100-85)2]=70,
S22班=![]() (70-85)2+(100-85)2+(100-85)2+(75-85)2+(80-85)2]=160,
(70-85)2+(100-85)2+(100-85)2+(75-85)2+(80-85)2]=160,
∵S21班<S22班,
∴八(1)班比八(2)班成绩更平稳一些.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
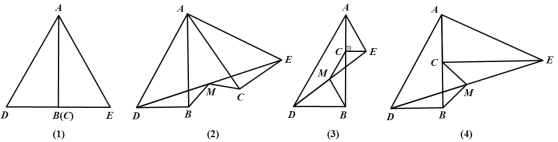
【题目】如图,将两个全等的直角三角形△ABD、△ACE拼在一起(图(1)).令△ABD不动,
(1)若将△ACE绕点A逆时针旋转,连接DE,M是DE的中点,连接MB、MC(图(2)),证明:MB=MC.
(2)若将图(1)中的CE向上平移,∠CAE不变,连接DE,M是DE的中点,连接MB、MC(图(3)),判断MB、MC的数量关系,并说明理由.
(3)在(2)中,若∠CAE的大小改变(图(4)),其他条件不变,则(2)中的MB、MC的数量关系还成立吗?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校七年级学生准备去购买《英汉词典》一书,此书标价为20元。现A、B两书店都有此书出售,A店按如下方法促销:若只购一本,则按标价销售;若一次性购买多于一本,但不多出20本时,每多购一本,每本销售价在标价的基础上优惠2%(例如买两本,每本价优惠2%;买三本价优惠4%,以此类推);若购买多于20本时,每本售价为12元,B店一律按标价的7折销售;
(1)试分别写出在两书店购此书的总价yA、yB与购本书数x之间的函数关系式.
(2)若某班一次性购买多于20本时,那么去哪家书店购买更合算?为什么?若要一次性购买不多于20本时,先写出y(y=yA-yB)与购书本数x之间的函数关系式,并在图中画出其函数图象,再利用函数图象分析去哪家书店购买更合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AD是边BC上的中线,过点A作AE∥BC,过点D作DE∥AB,DE与AC、AE分别交于点O、点E,连接EC.
(1)求证:AD=EC;
(2)当∠BAC=Rt∠时,求证:四边形ADCE是菱形.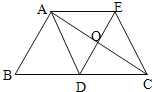
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个正整数能表示成两个连续偶数的平方差,那么这个正整数为“神秘数”.
如:![]()
![]()
![]()
因此,4,12,20这三个数都是神秘数.
(1)28和2012这两个数是不是神秘数?为什么?
(2)设两个连续偶数为![]() 和
和![]() (其中
(其中![]() 为非负整数),由这两个连续偶数构造的神秘数是4的倍数,请说明理由.
为非负整数),由这两个连续偶数构造的神秘数是4的倍数,请说明理由.
(3)两个连续奇数的平方差(取正数)是不是神秘数?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
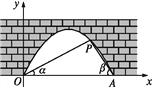
【题目】如图是抛物线型拱桥,P处有一照明灯,水面OA宽4 m,从O,A两处观测P处,仰角分别为α,β,且tan α=![]() ,tan β=
,tan β=![]() ,以O为原点,OA所在直线为x轴建立平面直角坐标系.
,以O为原点,OA所在直线为x轴建立平面直角坐标系.
(1)求点P的坐标.
(2)水面上升1 m,水面宽多少?(结果精确到0.1 m.参考数据: ![]() ≈1.41)
≈1.41)
查看答案和解析>>
科目:初中数学 来源: 题型:
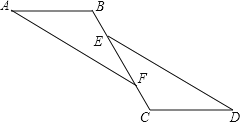
【题目】如图,已知:点B、E、F、C在同一直线上,∠A=∠D,BE=CF,且AB∥CD.求证:AF∥ED
证明:∵BE=FC
∴BE+EF=FC+EF(____________________________)
即:___________
∵AB∥CD
∴∠B=∠C(_________________________)
在△ABF和△DCE中,
∠A=∠D, ∠B=∠C, BF=CE
∴△ABF≌△DCE(________)
∴∠AFB=∠DEC(_________________________________)
∴AF∥ED(__________________________________)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com