
【题目】在一次羽毛球赛中,甲运动员在离地面![]() 米的P点处发球,球的运动轨迹PAN看作一个抛物线的一部分,当球运动到最高点A时,其高度为3米,离甲运动员站立地点O的水平距离为5米,球网BC离点O的水平距离为6米,以点O为原点建立如图所示的坐标系,乙运动员站立地点M的坐标为(m,0).
米的P点处发球,球的运动轨迹PAN看作一个抛物线的一部分,当球运动到最高点A时,其高度为3米,离甲运动员站立地点O的水平距离为5米,球网BC离点O的水平距离为6米,以点O为原点建立如图所示的坐标系,乙运动员站立地点M的坐标为(m,0).
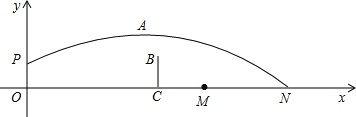
(1)求抛物线的解析式(不要求写自变量的取值范围);
(2)求羽毛球落地点N离球网的水平距离(即NC的长);
(3)乙原地起跳后可接球的最大高度为2.4米,若乙因为接球高度不够而失球,求m的取值范围.
【答案】(1)y=﹣![]() (x﹣5)2+3;(2)CN=3
(x﹣5)2+3;(2)CN=3![]() ﹣1(米);(3)m的取值范围为:6<m<8.
﹣1(米);(3)m的取值范围为:6<m<8.
【解析】
(1)设抛物线解析式为y=a(x5)2+3,将点(0,![]() )代入可得出a的值,继而得出抛物线解析式;
)代入可得出a的值,继而得出抛物线解析式;
(2)令y=0,可得出ON的长度,由NC=ONOC即可得出答案;
(3)先计算出刚好接到球时m的值,从而结合所给图形可得出运动员接球高度不够m的取值范围.
(1)设抛物线解析式为y=a(x﹣5)2+3,
将点(0,![]() )代入可得:
)代入可得:![]() =a(0﹣5)2+3,
=a(0﹣5)2+3,
解得:a=﹣![]() ,
,
故抛物线的解析式为:y=﹣![]() (x﹣5)2+3;
(x﹣5)2+3;
(2)当y=0时,﹣![]() (x﹣5)2+3=0,
(x﹣5)2+3=0,
解得:x1=5﹣3![]() (舍去),x2=5+3
(舍去),x2=5+3![]() ,
,
即ON=5+3![]() ,
,
∵OC=6,
∴CN=3![]() ﹣1(米);
﹣1(米);
(3)若运动员乙原地起跳到最大高度时刚好接到球,
此时﹣![]() (m﹣5)2+3=2.4,
(m﹣5)2+3=2.4,
解得:m1=2,m2=8,
∵运动员接球高度不够,
∴2<m<8,
∵OC=6,乙运动员接球时不能触网,
∴m的取值范围为:6<m<8.


 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案科目:初中数学 来源: 题型:
【题目】穿楼而过的轻轨、《千与千寻》现实版洪崖洞、空中巴士长江索道……,“3D魔幻城”吸引着海量游客前来重庆打卡.2018年的清明节和“五一”节,洪崖洞入围全球旅游热门目的地榜单,排名仅次于故宫.位于洪崖洞的重庆知名火锅小天鹅火锅在节日期间每天也人满为患,其中鸳鸯火锅和红汤火锅最受游客青睐.在清明节期间,前来就餐选择鸳鸯火锅和红汤火锅的游客共有2200名,鸳鸯火锅和红汤火锅的人均消费分别为130元和120元.
(1)清明节期间,若选择红汤火锅的人数不超过鸳鸯火锅人数的1.5倍.求至少有多少人选择鸳鸯火锅?
(2)“五一”节期间,因天气渐热的原因,前来就餐的游客人数有所下降,与(1)问中选择鸳鸯火锅的人数最少时相比,选择两种火锅的人数均下降了a%;人均消费与清明节期间相比均有所上升,其中鸳鸯火锅的人均消费上涨了a%,红汤火锅的人均消费上涨了![]() %,最终“五一”节期间两种火锅的总销售额与(1)问中选择鸳鸯火锅的人数最少时的两种火锅的总销售额持平,求a的值.
%,最终“五一”节期间两种火锅的总销售额与(1)问中选择鸳鸯火锅的人数最少时的两种火锅的总销售额持平,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)水果店张阿姨以每斤2元的价格购进某种水果若干斤,然后以每斤4元的价格出售,每天可售出100斤,通过调查发现,这种水果每斤的售价每降低0.1元,每天可多售出20斤,为保证每天至少售出260斤,张阿姨决定降价销售.
(1)若将这种水果每斤的售价降低x元,则每天的销售量是 斤(用含x的代数式表示);
(2)销售这种水果要想每天盈利300元,张阿姨需将每斤的售价降低多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
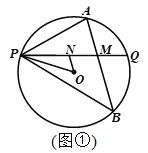
【题目】已知P是⊙O上一点,过点P作不过圆心的弦PQ,在劣弧PQ和优弧PQ上分别有动点A、B(不与P,Q重合),连接AP、BP. 若∠APQ=∠BPQ.
(1)如图1,当∠APQ=45°,AP=1,BP=2![]() 时,求⊙O的半径;
时,求⊙O的半径;
(2)如图2,选接AB,交PQ于点M,点N在线段PM上(不与P、M重合),连接ON、OP,若∠NOP+2∠OPN=90°,探究直线AB与ON的位置关系,并证明.
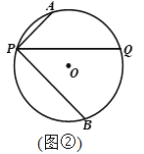
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,先将抛物线y=2x2﹣4x关于y轴作轴对称变换,再将所得的抛物线,绕它的顶点旋转180°,那么经两次变换后所得的新抛物线的函数表达式为( )
A.y=﹣2x![]() ﹣4xB.y=﹣2x
﹣4xB.y=﹣2x![]() +4x
+4x
C.y=﹣2x![]() ﹣4x﹣4D.y=﹣2x
﹣4x﹣4D.y=﹣2x![]() +4x+4
+4x+4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是
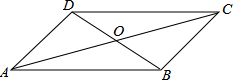
A.AB∥DC,AD∥BC B.AB=DC,AD=BC
C.AO=CO,BO=DO D.AB∥DC,AD=BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A1的坐标为(2,0),过点A1作x轴的垂线交直线l:y=![]() x于点B1,以原点O为圆心,OB1的长为半径画弧交x轴正半轴于点A2,则点A2的坐标为_____;再过点A2作x轴的垂线交直线l于点B2,以原点O为圆心,以OB2的长为半径画弧交x轴正半轴于点A3;….按此作法进行下去,则
x于点B1,以原点O为圆心,OB1的长为半径画弧交x轴正半轴于点A2,则点A2的坐标为_____;再过点A2作x轴的垂线交直线l于点B2,以原点O为圆心,以OB2的长为半径画弧交x轴正半轴于点A3;….按此作法进行下去,则![]() 的长是_____.
的长是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】投资1万元围一个矩形菜园(如图),其中一边靠墙,另外三边选用不同材料建造.墙长24 m,平行于墙的边的费用为200元/m,垂直于墙的边的费用为150元/m,设平行于墙的边长为x m.
(1)设垂直于墙的一边长为y m,直接写出y与x之间的函数关系式;
(2)若菜园面积为384 m2,求x的值;
(3)求菜园的最大面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com