
【题目】在平面直角坐标系中,点O为坐标原点,点B和点C分别是x轴的正半轴和y轴的正半轴上的两点,且OB:BC=1:![]() ,直线BC的解析式为y=﹣kx+6k(k≠0).
,直线BC的解析式为y=﹣kx+6k(k≠0).
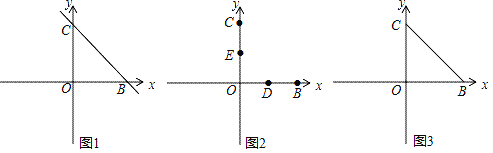
(1)如图1,求点C的坐标;
(2)如图2,点D为OB中点,点E为OC中点,点F在y轴的负半轴上,点A是射线FD上的第一象限的点,连接AE、ED,若FD=DA,且S△AED=![]() ,求点A的坐标;
,求点A的坐标;
(3)如图3,在(2)的条件下,点P在线段OB上,点Q在线段OC的延长线上,CQ=BP,连接PQ与BC交于点M,连接AM并延长AM到点N,连接QN、AP、AB和NP,若∠QPA﹣∠NQO=∠NQP﹣∠PAB,NP=2![]() ,求直线PQ的解析式.
,求直线PQ的解析式.
【答案】(1)C(0,6);(2)A(6,6);(3)直线PQ的解析式y=﹣2x+8.
【解析】
(1)先求出OB=6,进而求出BC=6![]() ,最后用勾股定理求出OC=6,即可得出结论;
,最后用勾股定理求出OC=6,即可得出结论;
(2)先判断出△FDO≌△ADB,进而求出点A的横坐标为6,进而利用面积差求出EF=9即可得出结论;
(3)先判断出四边形ACOB是平行四边形,进而判断出平行四边形ACOB是正方形,再判断出PT=PB=CQ,进而得出△PTM≌△QCM,再判断出∠NQP=∠APQ,进而判断出△NMQ≌△AMP,即可判断出四边形QNPA是平行四边形,再判断出平行四边形QNPA是正方形,进而求出P(4,0),Q(0,8),即可得出结论.
解:(1)令y=0,则﹣kx+6k=0,
∵k≠0,
∴x=6,
∴B(6,0),
∴OB=6,
∵OB:BC=1:![]() ,
,
∴BC=6![]() ,
,
在Rt△BOC中,OB2+OC2=BC2,
∴OC=6,
∴C(0,6);
(2)如图2,连接AB,过点A作AH⊥y轴于H,
∵FD=DA,OD=BD,∠ODF=∠BDA,
∴△FDO≌△ADB,
∴∠FOD=∠ABD=90°,OF=AB,
∴AB⊥x轴,
∴点A的横坐标为6,
∴S△AED=S△AEF﹣S△DEF=![]() AH﹣
AH﹣![]() EFOD=
EFOD=![]() EF(AH﹣OD)=
EF(AH﹣OD)=![]() EFBD,
EFBD,
∵S△AED=![]() ,BD=3,
,BD=3,
∴EF=9,
∵EO=3,
∴OF=6,
∴BA=6,
∴A(6,6);
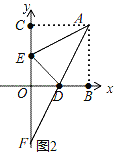
(3)如图3,过点P作PT∥y轴,交BC于T,连接AQ,AC,
∴∠MPT=∠MQC,
∵AB∥OC,AB=OC,
∴四边形ACOB是平行四边形,
∵∠COB=90°,OB=OC,
∴平行四边形ACOB是正方形,
∴∠ACO=90°,
∴∠ACQ=90°,
∵OB=OC,
∴∠OCB=∠OBC=45°,
∴∠PBT=∠PTB=45°,
∴PT=PB=CQ,
∵∠PMT=∠QMC,
∴△PTM≌△QCM,
∴PM=QM,
∵BA∥y轴,PT∥y轴,
∴AB∥PT,
∴∠BAP=∠TPA,
∵∠QPA﹣∠NQO=∠NQP﹣∠PAB,
∴∠QPT+∠TPA﹣∠NQO=∠NQO+∠OQP﹣∠PAB,
∴∠TPA=∠NQO,
∴∠NQP=∠APQ,
∵∠NMQ=∠AMP,
∴△NMQ≌△AMP,
∴NM=AM,
∵MQ=MP,
∴四边形QNPA是平行四边形,
∵AC=AB,∠QCA=∠PBA=90°,CQ=BP,
∴△QCA≌△PBA,
∴AQ=AP,∠QAC=∠PAB,
∴∠QAP=∠CAB=90°,
∴QNPA是正方形,
∴NP=AP=2![]() ,
,
在Rt△ABP中,AP2=AB2+PB2,
∴PB=2,
∴OP=OB﹣PB=4,OQ=OC+QC=8,
∴P(4,0),Q(0,8),
∴直线PQ的解析式y=﹣2x+8.


科目:初中数学 来源: 题型:
【题目】如图,海中一小岛有一个观测点A,某天上午观测到某渔船在观测点A的西南方向上的B处跟踪鱼群由南向北匀速航行.B处距离观测点30 ![]() 海里,若该渔船的速度为每小时30海里,问该渔船多长时间到达观测点A的北偏西60°方向上的C处?(计算结果用根号表示,不取近似值)
海里,若该渔船的速度为每小时30海里,问该渔船多长时间到达观测点A的北偏西60°方向上的C处?(计算结果用根号表示,不取近似值)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸上的每个小方格都是边长为1的正方形,△ABC 的顶点均在格点上,若 B
点的坐标为(-4,-2), 按要求回答下列问题:
(1)在图中建立正确的平面直角坐标系;
(2)根据所建立的坐标系,写出点A和点C的坐标;
(3)画出△ABC关于x轴的对称图形△ABC;
(4)△ABC 的面积为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC为等边三角形,∠ABC、∠ACB的平分线相交于点O,OE∥AB交BC于点E,OF∥AC交BC于点F,图中等腰三角形共有( )
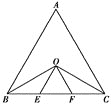
A. 6个 B. 5个 C. 4个 D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某剧院的观众席的座位为扇形,且按下列分式设置:
排数(x) | 1 | 2 | 3 | 4 | … |
座位数(y) | 50 | 53 | 56 | 59 | … |
(1)按照上表所示的规律,当x每增加1时,y如何变化?
(2)写出座位数y与排数x之间的关系式;
(3)按照上表所示的规律,某一排可能有90个座位吗?说说你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA的中点,点P在BC上运动,当△ODP是腰长为5的等腰三角形时,则P点的坐标为 . 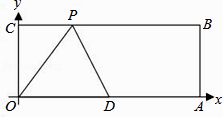
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,下列能判定AB∥CD的条件有( )个.
(1)∠B+∠BCD=180°;(2)∠1=∠2;(3)∠3=∠4;(4)∠B=∠5.

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com