
如图,△ABC中,AB AC,AB的垂直平分线DE交AC于D,交AB于E,且BD平分∠ABC,则∠BDC=___________度.
AC,AB的垂直平分线DE交AC于D,交AB于E,且BD平分∠ABC,则∠BDC=___________度.
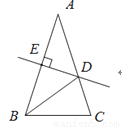
科目:初中数学 来源:山东省德州地区2017-2018学年度九年级第一学期期末检测数学试卷 题型:填空题
用等腰直角三角板画∠AOB=45°,将三角板沿OB方向平移到如图所示的虚线M处后绕点M逆时针旋转22°,则三角板的斜边与射线OA的夹角α为_____度.

查看答案和解析>>
科目:初中数学 来源:2018人教版九年级数学下册练习:第二十八章 达标检测卷 题型:解答题
如图,在四边形ABCD中,∠B=∠D=90°,AB=BC,AD=7,tan A=2.求CD的长.

查看答案和解析>>
科目:初中数学 来源:2018人教版九年级数学下册练习:第二十八章 达标检测卷 题型:单选题
在Rt△ABC中,∠C=90°,AB=10,AC=6,则cos A的值是( )
A. 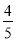 B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源:河南省周口市西华县2017-2018学年八年级上学期期末考试数学试卷 题型:解答题
AD,AE分别是△ABC的高和角平分线.

(1)已知∠B=30°,∠C=60°,求∠DAE的度数;
(2)设∠B= x,∠C= y(x < y),请直接写出∠DAE的度数 .(用含x ,y的代数式表示)
(1)∠EAD=15°;(2) ∠EAD= (y-x) 【解析】分析:分析:(1)根据三角形内角和定理求出∠BAC,再根据角平分线的定义求出∠EAC,根据直角三角形两锐角互余求出∠DAC,然后求解即可.(2)同(1)即可得出结果. 本题解析: (1) 由 ∴ 又AE平分, ∴ ∴ (2)查看答案和解析>>
科目:初中数学 来源:河南省周口市西华县2017-2018学年八年级上学期期末考试数学试卷 题型:单选题
如图,直线l外有不重合的两点A、B.在直线l上求一点C,使得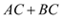 的长度最短,作法为:①作点B关于直线l的对称点B'.②连接AB'交直线l于点C,则点C即为所求.在解决这个问题时,没有用到的知识点是( )
的长度最短,作法为:①作点B关于直线l的对称点B'.②连接AB'交直线l于点C,则点C即为所求.在解决这个问题时,没有用到的知识点是( )

A. 线段的垂直平分线性质 B. 两点之间线段最短
C. 三角形两边之和大于第三边 D. 角平分线的性质
D 【解析】【解析】 ∵点B和点B′关于直线l对称,且点C在l上, ∴CB=CB′. ∵AB′交l于C,且两条直线相交只有一个交点, ∴CB′+CA=AB′,即CA+CB=AB′. 任取直线l上一点C′,与点C不重合,则C′B′+C′A>AB′, 即AB′是CA+CB的最小值. 本题在解答过程中利用了线段垂直平分线的性质定理:两点之间,线段最短,体现了转化思想...查看答案和解析>>
科目:初中数学 来源:河南省周口市西华县2017-2018学年八年级上学期期末考试数学试卷 题型:单选题
分式 可变形为( )
可变形为( )
A. 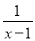 B.
B.  C.
C. 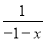 D.
D. 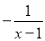
查看答案和解析>>
科目:初中数学 来源:2017-2018学年七年级数学北师大版上册 第1章 丰富的图形世界 单元测试卷 题型:单选题
下列四张正方形硬纸片,剪去阴影部分后,如果沿虚线折叠,可以围成一个封闭的长方体包装盒的是( )
A. B.
B.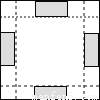 C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源:广东省汕头市澄海区2017-2018学年八年级上学期期末质量检测数学试卷 题型:解答题
两个大小不同的等腰直角三角板如图①所示放置,图②是由它抽象出来的几何图形,点B、C、E在同一条直线上,连结DC.
(1)请找出图②中的全等三角形,并给予证明;
(2)求证:DC⊥BE.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com