
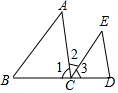
 如图,点C在BD上,请分别根据已知条件进行推理,并在括号内注明推理根据.
如图,点C在BD上,请分别根据已知条件进行推理,并在括号内注明推理根据.分析 (1)根据同位角相等,两直线平行可得AB∥CE;
(2)根据同位角相等,两直线平行可得AC∥ED;
(3)根据内错角相等,两直线平行可得AB∥CE;
(4)根据同旁内角互补,两直线平行可得AB∥CE.
解答 解:(1)∵∠B=∠3(已知),
∴AB∥CE(同位角相等,两直线平行),
故答案为:AB;CE;同位角相等,两直线平行;
(2)∵∠1=∠D(已知),
∴AC∥ED(同位角相等,两直线平行);
故答案为:AC;DE;同位角相等,两直线平行;
(3)∵∠2=∠A(已知),
∴AB∥CE(内错角相等,两直线平行),
故答案为:AB;CE;内错角相等,两直线平行;
(4)∵∠B+∠BCE=180°(已知),
∴AB∥CE(同旁内角互补,两直线平行),
故答案为:AB;CE;同旁内角互补,两直线平行.
点评 此题主要考查了平行线的判定,关键是掌握平行线的判定定理.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某数学兴趣小组为了估计河的宽度,在河对岸选定一个8标点P,在近岸取点Q和S,使点P,Q,S共线且直找PS与河垂直,接着在过点S且与PS垂直的直线a上选择适当的点T,确定PT与过点Q且垂直PS的直线b的交点R.如果测得QS=45m,ST=90m,QS=60m,请计算河的宽度PQ.
某数学兴趣小组为了估计河的宽度,在河对岸选定一个8标点P,在近岸取点Q和S,使点P,Q,S共线且直找PS与河垂直,接着在过点S且与PS垂直的直线a上选择适当的点T,确定PT与过点Q且垂直PS的直线b的交点R.如果测得QS=45m,ST=90m,QS=60m,请计算河的宽度PQ.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (x-1)(x+2) | B. | (x-1)(x-2) | C. | (x+1)(x+2) | D. | (x+1)(x-2) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -3x2+6xy-3y2 | B. | 3x2-6xy-y2 | C. | 3x2-6xy+3y2 | D. | -3x2-6xy-3y2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在平面直角坐标系中,点A(0,4$\sqrt{3}$),B(m,-2$\sqrt{3}$),C(n,-2$\sqrt{3}$),且m,n满足$\sqrt{m+3n}$+(n-6)2=0,线段BC交y轴于点H.
在平面直角坐标系中,点A(0,4$\sqrt{3}$),B(m,-2$\sqrt{3}$),C(n,-2$\sqrt{3}$),且m,n满足$\sqrt{m+3n}$+(n-6)2=0,线段BC交y轴于点H.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com