
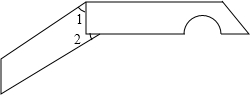
 如图,是我们生活中经常接触的小刀,刀柄是一个直角梯形(挖去一个半圆),刀片上下是平行的,转动刀片时会形成∠1、∠2,则∠1+∠2=90°.
如图,是我们生活中经常接触的小刀,刀柄是一个直角梯形(挖去一个半圆),刀片上下是平行的,转动刀片时会形成∠1、∠2,则∠1+∠2=90°.  新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x(x+1)=28 | B. | x(x-1)=28×2 | C. | x(x+1)=28 | D. | x(x-1)=28 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
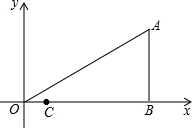 如图,在平面直角坐标系中,已知Rt△ABO的顶点B在x轴正半轴上,∠AOB=30?,OA=2$\sqrt{3}$,C($\frac{1}{2}$,0),P 为OA上的一个动点,
如图,在平面直角坐标系中,已知Rt△ABO的顶点B在x轴正半轴上,∠AOB=30?,OA=2$\sqrt{3}$,C($\frac{1}{2}$,0),P 为OA上的一个动点,查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 如果a=b,那么a-c=b-c | B. | 如果$\frac{a}{c}=\frac{b}{c}$,那么a=b | ||
| C. | 如果ac2=bc2,那么a=b | D. | 如果a(c2+1)=b(c2+1),那么a=b |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
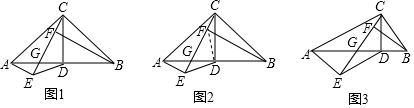
| A. | $\frac{AE}{AC}=\frac{1}{2}$ | B. | $\frac{DE}{BC}=\frac{1}{3}$ | C. | $\frac{AE}{AC}=\frac{1}{3}$ | D. | $\frac{DE}{BC}=\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com