
分析 (1)根据题意设出y与x的关系式即可;
(2)把y=-2代入解析式求出x的值即可;
(2)把y=10代入解析式求出x的值即可.
解答 解:(1)因为y与x-3成反比例,可得:$y=\frac{k}{x-3}$,
把x=4,y=5代入$\frac{k}{4-3}=5$,
解得:k=5,
所以解析式为:$y=\frac{5}{x-3}$,
(2)把y=-2代入$y=\frac{5}{x-3}$,可得:$-2=\frac{5}{x-3}$,
解得:x=0.5;
(3)把y=10代入$y=\frac{5}{x-3}$,可得:$10=\frac{5}{x-3}$,
解得:x=3.5.
点评 此题考查了待定系数法求反比例函数解析式,熟练掌握待定系数法是解本题的关键.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:初中数学 来源: 题型:解答题
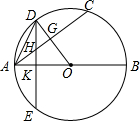 如图,AB是⊙O的直径,AC为⊙O的弦,半径0D⊥AC于G.弦DE⊥AB于K,交AC于H.
如图,AB是⊙O的直径,AC为⊙O的弦,半径0D⊥AC于G.弦DE⊥AB于K,交AC于H.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,CD为⊙O的弦,在CD上取CE=DF,连结OE、OF,并延长交⊙O于点A、B.
如图所示,CD为⊙O的弦,在CD上取CE=DF,连结OE、OF,并延长交⊙O于点A、B.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com