
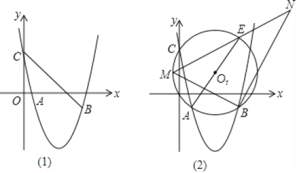
”¾ĢāÄæ”æÅ×ĪļĻßy=ax+bx+4£Øa”Ł0£©¹żµćA(1, ©1)£¬B(5, ©1)£¬ÓėyÖį½»ÓŚµćC.
£Ø1£©ĒóÅ×ĪļĻß±ķ“ļŹ½£»
£Ø2£©ČēĶ¼1£¬Į¬½ÓCB£¬ŅŌCBĪŖ±ß×÷CBPQ£¬ČōµćPŌŚÖ±ĻßBCĻĀ·½µÄÅ×ĪļĻßÉĻ£¬QĪŖ×ų±źĘ½ĆęÄŚµÄŅ»µć£¬ĒŅCBPQµÄĆ껿ĪŖ30£¬
¢ŁĒóµćP×ų±ź;
¢Ś¹ż“Ė¶žµćµÄÖ±Ļß½»yÖįÓŚF, “ĖÖ±ĻßÉĻŅ»¶ÆµćG,µ±GB+![]() ×īŠ”Ź±,ĒóµćG×ų±ź.
×īŠ”Ź±,ĒóµćG×ų±ź.
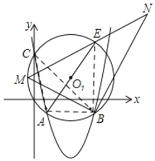
£Ø3£©ČēĶ¼2£¬”ŃO1¹żµćA”¢B”¢CČżµć£¬AEĪŖÖ±¾¶£¬µćMĪŖ ÉĻµÄŅ»¶Æµć£Ø²»ÓėµćA£¬EÖŲŗĻ£©£¬”ĻMBNĪŖÖ±½Ē£¬±ßBNÓėMEµÄŃÓ³¤Ļß½»ÓŚN£¬ĒóĻ߶ĪBN³¤¶ČµÄ×ī“óÖµ
”¾“š°ø”æ£Ø1£©y=x©6x+4£Ø2£©¢ŁP(2, -4)»ņP(3, -5) ¢ŚG(0, -2)£Ø3£©![]()
”¾½āĪö”æ
£Ø1£©°ŃµćA£Ø1£¬-1£©£¬B£Ø5£¬-1£©“śČėÅ×ĪļĻßy=ax2+bx+4½āĪöŹ½£¬¼“æÉµĆ³öÅ×ĪļĻߵıķ“ļŹ½£»
£Ø2£©¢ŁČēĶ¼£¬Į¬½ÓPC£¬¹żµćP×÷yÖįµÄĘ½ŠŠĻß½»Ö±ĻßBCÓŚR£¬æÉĒóµĆÖ±ĻßBCµÄ½āĪöŹ½ĪŖ£ŗy=-x+4£¬ÉčµćP£Øt£¬t2-6t+4£©£¬R£Øt£¬-t+4£©£¬ŅņĪŖCBPQµÄĆ껿ĪŖ30£¬ĖłŅŌS”÷PBC=![]() ”Į(t+4t2+6t4)”Į5£½15£¬½āµĆtµÄÖµ£¬¼“æÉµĆ³öµćPµÄ×ų±ź£»¢Śµ±µćPĪŖ£Ø2£¬-4£©Ź±£¬ĒóµĆÖ±ĻßQPµÄ½āĪöŹ½ĪŖ£ŗy=-x-2£¬µĆF£Ø0£¬-2£©£¬”ĻGOR=45”ć£¬ŅņĪŖGB+
”Į(t+4t2+6t4)”Į5£½15£¬½āµĆtµÄÖµ£¬¼“æÉµĆ³öµćPµÄ×ų±ź£»¢Śµ±µćPĪŖ£Ø2£¬-4£©Ź±£¬ĒóµĆÖ±ĻßQPµÄ½āĪöŹ½ĪŖ£ŗy=-x-2£¬µĆF£Ø0£¬-2£©£¬”ĻGOR=45”ć£¬ŅņĪŖGB+![]()
GF=GB+GR£¬ĖłŅŌµ±GÓŚFÖŲŗĻŹ±£¬GB+GR×īŠ”£¬¼“æÉµĆ³öµćGµÄ×ų±ź£»µ±µćPĪŖ£Ø3£¬-5£©Ź±£¬Ķ¬ĄķæÉĒó£»
£Ø3£©ĻČÓĆĆ껿·ØĒó³ösin”ĻACB=![]() £¬tan”ĻACB=
£¬tan”ĻACB=![]() £¬ŌŚRt”÷ABEÖŠ£¬ĒóµĆŌ²µÄÖ±¾¶£¬ŅņĪŖMB”ĶNB£¬æɵƔĻN=”ĻAEB=”ĻACB£¬ŅņĪŖtanN=
£¬ŌŚRt”÷ABEÖŠ£¬ĒóµĆŌ²µÄÖ±¾¶£¬ŅņĪŖMB”ĶNB£¬æɵƔĻN=”ĻAEB=”ĻACB£¬ŅņĪŖtanN=![]() £½
£½![]() £¬ĖłŅŌBN=
£¬ĖłŅŌBN=![]() MB£¬µ±MBĪŖÖ±¾¶Ź±£¬BNµÄ³¤¶Č×ī“ó£®
MB£¬µ±MBĪŖÖ±¾¶Ź±£¬BNµÄ³¤¶Č×ī“ó£®
(1) ½ā£ŗ£Ø1£©”ßÅ×ĪļĻßy=ax2+bx+4£Øa”Ł0£©¹żµćA£Ø1£¬-1£©£¬B£Ø5£¬-1£©£¬
”ą![]() ½āµĆ
½āµĆ![]()
”ąÅ×ĪļĻß±ķ“ļŹ½ĪŖy=x©6x+4£®
(2)¢ŁČēĶ¼£¬Į¬½ÓPC£¬¹żµćP×÷yÖįµÄĘ½ŠŠĻß½»Ö±ĻßBCÓŚR£¬
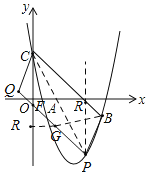
ÉčÖ±ĻßBCµÄ½āĪöŹ½ĪŖy=kx+m£¬
”ßB£Ø5£¬-1£©£¬C£Ø0£¬4£©£¬
”ą![]() £¬½āµĆ
£¬½āµĆ![]()
”ąÖ±ĻßBCµÄ½āĪöŹ½ĪŖ£ŗy=-x+4£¬
ÉčµćP£Øt£¬t2-6t+4£©£¬R£Øt£¬-t+4£©£¬
”ßCBPQµÄĆ껿ĪŖ30£¬
”ąS”÷PBC=![]() ”Į(t+4t2+6t4)”Į5£½15£¬
”Į(t+4t2+6t4)”Į5£½15£¬
½āµĆt=2»ņt=3£¬µ±t=2Ź±£¬y=-4
µ±t=3Ź±£¬y=-5£¬
”ąµćP×ų±źĪŖ£Ø2£¬-4£©»ņ£Ø3£¬-5£©£»
¢Śµ±µćPĪŖ£Ø2£¬-4£©Ź±£¬
”ßÖ±ĻßBC½āĪöŹ½ĪŖ£ŗy=-x+4£¬QP”ĪBC£¬
ÉčÖ±ĻßQPµÄ½āĪöŹ½ĪŖ£ŗy=-x+n£¬
½«µćP“śČė£¬µĆ-4=-2+n£¬n=-2£¬
”ąÖ±ĻßQPµÄ½āĪöŹ½ĪŖ£ŗy=-x-2£¬
”ąF£Ø0£¬-2£©£¬”ĻGOR=45”ć£¬
”ąGB+![]() GF=GB+GR
GF=GB+GR
µ±GÓŚFÖŲŗĻŹ±£¬GB+GR×īŠ”£¬“ĖŹ±µćGµÄ×ų±źĪŖ£Ø0£¬-2£©£¬
Ķ¬Ąķ£¬µ±µćPĪŖ£Ø3£¬-5£©Ź±£¬Ö±ĻßQPµÄ½āĪöŹ½ĪŖ£ŗy=-x-2£¬
Ķ¬ĄķæɵƵćGµÄ×ų±źĪŖ£Ø0£¬-2£©£¬
(3) £©”ßA£Ø1£¬-1£©£¬B£Ø5£¬-1£©C£Ø0£¬4£©£¬
”ąAC=![]() £¬BC=5
£¬BC=5![]() £¬
£¬
”ßS”÷ABC=![]() AC”ĮBCsin”ĻACB£½
AC”ĮBCsin”ĻACB£½![]() AB”Į5£¬
AB”Į5£¬
”ąsin”ĻACB=![]() £¬tan”ĻACB=
£¬tan”ĻACB=![]() £¬
£¬
”ßAEĪŖÖ±¾¶£¬AB=4£¬
”ą”ĻABE=90”ć£¬
”ßsin”ĻAEB=sin”ĻACB=![]() £½
£½![]() £¬
£¬
”ąAE=2![]() £¬
£¬
”ßMB”ĶNB£¬”ĻNMB=”ĻEAB£¬
”ą”ĻN=”ĻAEB=”ĻACB£¬
”ątanN=![]() £½
£½![]() £¬
£¬
”ąBN=![]() MB£¬
MB£¬
µ±MBĪŖÖ±¾¶Ź±£¬BNµÄ³¤¶Č×ī“ó£¬ĪŖ3![]() £®
£®


 ĘŚÄ©100·Ö“³¹Ųŗ£µķæ¼ĶõĻµĮŠ“š°ø
ĘŚÄ©100·Ö“³¹Ųŗ£µķæ¼ĶõĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
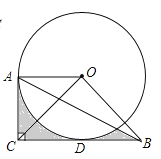
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖ”Ń![]() °ė¾¶ĪŖ
°ė¾¶ĪŖ![]() £¬“Ó”Ń
£¬“Ó”Ń![]() Ķāµć
Ķāµć![]() ×÷”Ń
×÷”Ń![]() µÄĒŠĻß
µÄĒŠĻß![]() ŗĶ
ŗĶ![]() £¬ĒŠµć·Ö±šĪŖµć
£¬ĒŠµć·Ö±šĪŖµć![]() ŗĶµć
ŗĶµć![]() £¬
£¬![]() £¬ŌņĶ¼ÖŠŅõÓ°²æ·ÖµÄĆ껿ŹĒ__________£®
£¬ŌņĶ¼ÖŠŅõÓ°²æ·ÖµÄĆ껿ŹĒ__________£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
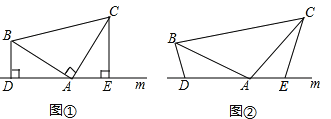
”¾ĢāÄæ”æ£Ø1£©ČēĶ¼¢Ł£¬ŅŃÖŖ£ŗŌŚ”÷ABCÖŠ£¬”ĻBAC£½90”ć£¬AB=AC£¬Ö±Ļßm¾¹żµćA£¬BD”ĶÖ±Ļßm, CE”ĶÖ±Ļßm,“¹×ć·Ö±šĪŖµćD”¢E.Ö¤Ć÷:DE=BD+CE.
£Ø2£©ČēĶ¼¢Ś£¬½«£Ø1£©ÖŠµÄĢõ¼žøÄĪŖ£ŗŌŚ”÷ABCÖŠ£¬AB=AC£¬D”¢A”¢EČżµć¶¼ŌŚÖ±ĻßmÉĻ,²¢ĒŅÓŠ”ĻBDA=”ĻAEC=”ĻBAC=¦Į,ĘäÖŠ¦ĮĪŖČĪŅā¶Ū½Ē.ĒėĪŹ½įĀŪDE=BD+CEŹĒ·ń³ÉĮ¢?Čē³ÉĮ¢,ĒėÄćøų³öÖ¤Ć÷;Čō²»³ÉĮ¢,ĒėĖµĆ÷ĄķÓÉ.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĪŖÅäŗĻ”°Ņ»“ųŅ»Ā·”±¹ś¼Ņ³«Ņ飬ijĢśĀ·»õŌĖ¼Æ×°ĻäĪļĮ÷Ō°ĒųÕżŹ½Ęō¶ÆĮĖ2ĘŚĄ©½Ø¹¤³ĢŅ»ĻīµŲ»ł»ł“”¼Ó¹Ģ“¦Ąķ¹¤³ĢÓÉ2”¢8Į½øö¹¤³Ģ¹«Ė¾³Šµ£½ØÉč£¬¼ŗÖŖ2¹¤³Ģ¹«Ė¾µ„¶Ą½ØÉčĶź³É“ĖĻī¹¤³ĢŠčŅŖ180Ģģ![]() ¹¤³Ģ¹«Ė¾µ„¶ĄŹ©¹¤Ģģŗó£¬
¹¤³Ģ¹«Ė¾µ„¶ĄŹ©¹¤Ģģŗó£¬![]() ¹¤³Ģ¹«Ė¾²ĪÓėŗĻ×÷£¬Į½¹¤³Ģ¹«Ė¾ÓÖ¹²Ķ¬Ź©¹¤
¹¤³Ģ¹«Ė¾²ĪÓėŗĻ×÷£¬Į½¹¤³Ģ¹«Ė¾ÓÖ¹²Ķ¬Ź©¹¤![]() ĢģŗóĶź³ÉĮĖ“ĖĻī¹¤³Ģ.
ĢģŗóĶź³ÉĮĖ“ĖĻī¹¤³Ģ.
£Ø1£©Ēó![]() ¹¤³Ģ¹«Ė¾µ„¶Ą½ØÉčĶź³É“ĖĻī¹¤³ĢŠčŅŖ¶ąÉŁĢģ£æ
¹¤³Ģ¹«Ė¾µ„¶Ą½ØÉčĶź³É“ĖĻī¹¤³ĢŠčŅŖ¶ąÉŁĢģ£æ
£Ø2£©ÓÉÓŚŹÜ¹¤³Ģ½ØÉč¹¤ĘŚµÄĻŽÖĘ£¬ĪļĮ÷Ō°Ēų¹ÜĪÆ»į¾ö¶Ø½«“ĖĻī¹¤³Ģ»®°ü³ÉĮ½²æ·Ö£¬ŅŖĒóĮ½¹¤³Ģ¹«Ė¾Ķ¬Ź±æŖ¹¤£¬![]() ¹¤³Ģ¹«Ė¾½ØÉčĘäÖŠŅ»²æ·ÖÓĆĮĖ
¹¤³Ģ¹«Ė¾½ØÉčĘäÖŠŅ»²æ·ÖÓĆĮĖ![]() ĢģĶź³É£¬
ĢģĶź³É£¬![]() ¹¤³Ģ¹«Ė¾½ØÉčĮķŅ»²æ·ÖÓĆĮĖ
¹¤³Ģ¹«Ė¾½ØÉčĮķŅ»²æ·ÖÓĆĮĖ![]() ĢģĶź³É£¬ĘäÖŠ
ĢģĶź³É£¬ĘäÖŠ![]() £¬
£¬![]() ¾łĪŖÕżÕūŹż£¬ĒŅ
¾łĪŖÕżÕūŹż£¬ĒŅ![]() £¬
£¬![]() £¬Ēó
£¬Ēó![]() ”¢
”¢![]() Į½øö¹¤³Ģ¹«Ė¾ø÷Ź©¹¤½ØÉčĮĖ¶ąÉŁĢģ£æ
Į½øö¹¤³Ģ¹«Ė¾ø÷Ź©¹¤½ØÉčĮĖ¶ąÉŁĢģ£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ½ńÄźŹĒĪŅŹŠČ«ĆęĶĘ½ųÖŠŠ”ѧŠ£”°Éē»įÖ÷ŅåŗĖŠÄ¼ŪÖµ¹Ū”±½Ģӿğ.ijŠ£¶ŌČ«Š£Ń§Éś½ųŠŠĮĖÖŠĘŚ¼ģ²āĘĄ¼Ū,¼ģ²ā½į¹ū·ÖĪŖ![]() (ÓÅŠć)”¢
(ÓÅŠć)”¢![]() £ØĮ¼ŗĆ£©”¢
£ØĮ¼ŗĆ£©”¢![]() £ØŗĻøń£©”¢
£ØŗĻøń£©”¢![]() £Ø²»ŗĻøń£©ĖÄøöµČ¼¶.²¢Ė껜³éČ”ČōøÉĆūѧɜµÄ¼ģ²ā½į¹ū×÷ĪŖŃł±¾½ųŠŠŹż¾Ż“¦Ąķ,ÖĘ×÷ĮĖČēĻĀĖłŹ¾²»ĶźÕūµÄĶ³¼Ę±ķ£ØĶ¼1£©ŗĶĶ³¼ĘĶ¼£ØĶ¼2£©.
£Ø²»ŗĻøń£©ĖÄøöµČ¼¶.²¢Ė껜³éČ”ČōøÉĆūѧɜµÄ¼ģ²ā½į¹ū×÷ĪŖŃł±¾½ųŠŠŹż¾Ż“¦Ąķ,ÖĘ×÷ĮĖČēĻĀĖłŹ¾²»ĶźÕūµÄĶ³¼Ę±ķ£ØĶ¼1£©ŗĶĶ³¼ĘĶ¼£ØĶ¼2£©.
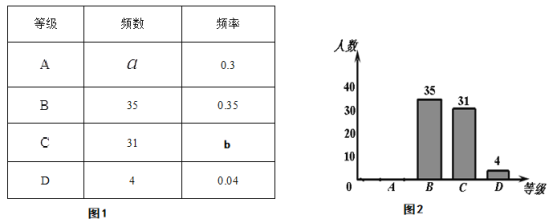
Ēėøł¾ŻĶ¼1”¢Ķ¼2Ģį¹©µÄŠÅĻ¢£¬½ā“šĻĀĮŠĪŹĢā£ŗ
£Ø1£©±¾“ĪĖ껜³éČ”µÄŃł±¾ČŻĮæĪŖ
£Ø2£©![]() ,
,![]() .
.
£Ø3£©ĒėŌŚĶ¼2ÖŠ²¹Č«ĢõŠĪĶ³¼ĘĶ¼.
£Ø4£©ČōøĆŠ£¹²ÓŠŃ§Éś800ČĖ£¬¾Ż“Ė¹ĄĖć£¬øĆŠ£Ń§ÉśŌŚ±¾“Ī¼ģ²āÖŠ“ļµ½”°![]() (ÓÅŠć)”±µČ¼¶µÄѧɜČĖŹżĪŖ ČĖ.
(ÓÅŠć)”±µČ¼¶µÄѧɜČĖŹżĪŖ ČĖ.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬AB£½AC£¬”ĻBAC£½45”ć£¬½«”÷ABCČʵćAÄꏱÕė·½ĻņŠż×ŖµĆ”÷AEF£¬ĘäÖŠ£¬E£¬FŹĒµćB£¬CŠż×ŖŗóµÄ¶ŌÓ¦µć£¬BE£¬CFĻą½»ÓŚµćD£®ČōĖıߊĪABDFĪŖĮāŠĪ£¬Ōņ”ĻCAEµÄ“󊔏Ē£Ø””””£©
![]()
A. 45”ćB. 60”ćC. 75”ćD. 90”ć
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æijŹŠŹµŹ©²śŅµ¾«×¼·öʶ£¬°ļ֜ʶĄ§»§³Š°ü»ÄɽÖÖÖ²Ä³Ę·ÖÖĆŪčÖ£®ŅŃÖŖøĆĆŪčֵijɱ¾¼ŪĪŖ6ŌŖ/Ē§æĖ£¬µ½ĮĖŹÕ»ń¼¾½ŚĶ¶ČėŹŠ³”ĻśŹŪŹ±£¬µ÷²éŹŠ³”ŠŠĒéŗ󣬷¢ĻÖøĆĆŪčÖ²»»įæ÷±¾£¬ĒŅĆæĢģµÄĻśŹŪĮæy£ØĒ§æĖ£©ÓėĻśŹŪµ„¼Ūx£ØŌŖ£©Ö®¼äµÄŗÆŹż¹ŲĻµČēĶ¼ĖłŹ¾£®
£Ø1£©ĒóyÓėxµÄŗÆŹż¹ŲĻµŹ½£¬²¢Š“³öxµÄȔֵ·¶Ī§£»
£Ø2£©µ±øĆĘ·ÖÖĆŪčֶؼŪĪŖ¶ąÉŁŹ±£¬ĆæĢģĻśŹŪ»ńµĆµÄĄūČó×ī“ó£æ×ī“óĄūČóŹĒ¶ąÉŁ£æ
£Ø3£©Ä³“åÅ©»§½ńÄź¹²²ÉÕŖĆŪčÖ12000Ē§æĖ£¬ČōøĆĘ·ÖÖĆŪčֵı£ÖŹĘŚĪŖ50Ģģ£¬°“ÕÕ£Ø2£©µÄĻśŹŪ·½Ź½£¬ÄÜ·ńŌŚ±£ÖŹĘŚÄŚČ«²æĻśŹŪĶźÕāÅśĆŪčÖ£æČōÄÜ£¬ĒėĖµĆ÷ĄķÓÉ£»Čō²»ÄÜ£¬Ó¦¶ØĻśŹŪ¼ŪĪŖ¶ąÉŁŌŖŹ±£¬¼ČÄÜĻśŹŪĶźÓÖÄÜ»ńµĆ×ī“óĄūČó£æ

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ¹ŲÓŚxµÄ·½³Ģ£Øx©3£©£Øx©5£©=m£Øm£¾0£©ÓŠĮ½øöŹµŹżøł¦Į£¬¦Ā£Ø¦Į£¼¦Ā£©£¬ŌņĻĀĮŠŃ”ĻīÕżČ·µÄŹĒ£Ø””””£©
A. 3£¼¦Į£¼¦Ā£¼5 B. 3£¼¦Į£¼5£¼¦Ā C. ¦Į£¼2£¼¦Ā£¼5 D. ¦Į£¼3ĒŅ¦Ā£¾5
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬½«”÷ABCČʵćCĖ³Ź±ÕėŠż×Ŗ90”ćµĆµ½”÷EDC£®ČōµćA£¬D£¬EŌŚĶ¬Ņ»ĢõÖ±ĻßÉĻ£¬”ĻACB=20”ć£¬Ōņ”ĻADCµÄ¶ČŹżŹĒ![]() ””””
””””![]()

A. 55”ć B. 60”ć C. 65”ć D. 70”ć
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com