
 如图所示,把矩形ABCD沿EF对折后,使四边形ABFE与四边形GHFE重合,∠α=50°,求∠AEF的度数.
如图所示,把矩形ABCD沿EF对折后,使四边形ABFE与四边形GHFE重合,∠α=50°,求∠AEF的度数.

 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:初中数学 来源: 题型:
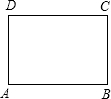 若一个矩形的短边与长边的比值为
若一个矩形的短边与长边的比值为
| ||
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 矩形ABCD在坐标系中的位置如图所示,若矩形的边长AB为1,AD为2,则点A,B,C,D的坐标依次为
矩形ABCD在坐标系中的位置如图所示,若矩形的边长AB为1,AD为2,则点A,B,C,D的坐标依次为查看答案和解析>>
科目:初中数学 来源:数学教研室 题型:013
如图所示,把矩形纸片ABCD对折后再展开,折痕为MN,再把D点叠在折痕MN上,得到 ,延长
,延长 交AB于F,则△EAF是
交AB于F,则△EAF是
[ ]

查看答案和解析>>
科目:初中数学 来源: 题型:013
如图所示,把矩形纸片ABCD对折后再展开,折痕为MN,再把D点叠在折痕MN上,得到 ,延长
,延长 交AB于F,则△EAF是
交AB于F,则△EAF是
[ ]

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com