
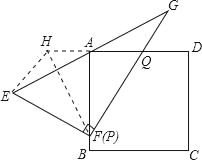
【题目】已知,如图:正方形ABCD,将Rt△EFG斜边EG的中点与点A重合,直角顶点F落在正方形的AB边上,Rt△EFG的两直角边分别交AB、AD边于P、Q两点,(点P与点F重合),如图1所示:



(1)求证:EP2+GQ2=PQ2;
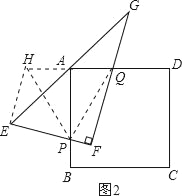
(2)若将Rt△EFG绕着点A逆时针旋转α(0°<α≤90°),两直角边分别交AB、AD边于P、Q两点,如图2所示:判断四条线段EP、PF、FQ、QG之间是否存在什么确定的相等关系?若存在,证明你的结论.若不存在,请说明理由;
(3)若将Rt△EFG绕着点A逆时针旋转α(90°<α<180°),两直角边所在的直线分别交BA、AD两边延长线于P、Q两点,并判断四条线段EP、PF、FQ、QG之间存在何种确定的相等关系?按题意完善图3,请直接写出你的结论(不用证明).
【答案】(1)见解析;(2)PF2+FQ2=EP2+GQ2;(3)四条线段EP、PF、FQ、QG之间的关系为PF2+GQ2=PE2+FQ2.
【解析】
(1)过点E作EH∥FG,由此可证△EAH≌△GAQ,然后根据全等三角形的性质得到EH=QG,又PQ=PH,在Rt△EPH中,EP2+EH2=PH2,由此可以得到EP2+GQ2=PQ2;
(2)过点E作EH∥FG,交DA的延长线于点H,连接PQ、PH,由此可证△EAH≌△GAQ,然后根据全等三角形的性质得到EH=QG,又PH=PQ,在Rt△EPH中,EP2+EH2=PH2,即EP2+GQ2=PH2,在Rt△PFQ中,PF2+FQ2=PQ2,故PF2+FQ2=EP2+GQ2;
(3)四条线段EP、PF、FQ、QG之间的关系为PE2+GQ2=PF2+FQ2,证明方法同上.
(1)过点E作EH∥FG,连接AH、FH,如图所示:
∵EA=AG,∠HEA=∠AGQ,∠HAE=∠GAD,
∴△EAH≌△GAQ,
∴EH=QG,HA=AQ,
∵FA⊥AD,
∴PQ=PH.
在Rt△EPH中,
∵EP2+EH2=PH2,
∴EP2+GQ2=PQ2;
(2)过点E作EH∥FG,交DA的延长线于点H,连接PQ、PH,
∵EA=AG,∠HEA=∠AGQ,∠HAE=∠GAD,
∴△EAH≌△GAQ,
∴EH=QG,HA=AQ,
∵PA⊥AD,
∴PQ=PH.
在Rt△EPH中,
∵EP2+EH2=PH2,
∴EP2+GQ2=PH2.
在Rt△PFQ中,
∵PF2+FQ2=PQ2,
∴PF2+FQ2=EP2+GQ2.
(3)四条线段EP、PF、FQ、QG之间的关系为PF2+GQ2=PE2+FQ2.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
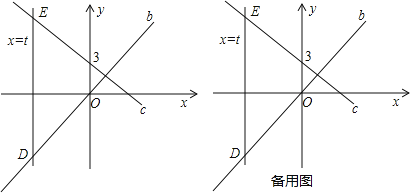
【题目】如图,已知直线c和直线b相较于点![]() ,直线c过点
,直线c过点![]() 平行于y轴的动直线a的解析式为
平行于y轴的动直线a的解析式为![]() ,且动直线a分别交直线b、c于点D、
,且动直线a分别交直线b、c于点D、![]() 在D的上方
在D的上方![]() .
.
![]() 求直线b和直线c的解析式;
求直线b和直线c的解析式;
![]() 若P是y轴上一个动点,且满足
若P是y轴上一个动点,且满足![]() 是等腰直角三角形,求点P的坐标.
是等腰直角三角形,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个圆柱形玻璃杯高![]() ,底面周长为
,底面周长为![]() ,有一只蚂蚁在一侧距下底
,有一只蚂蚁在一侧距下底![]() 的外侧
的外侧![]() 点,与点
点,与点![]() 正对的容器内侧距下底
正对的容器内侧距下底![]() 的
的![]() 点处有一饭粒,蚂蚁想吃
点处有一饭粒,蚂蚁想吃![]() 处的饭粒,要从杯子的外侧爬到杯子的内侧,杯子的厚度忽略不计,则至少需要爬________________
处的饭粒,要从杯子的外侧爬到杯子的内侧,杯子的厚度忽略不计,则至少需要爬________________![]() 。
。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图△ABC中,∠BAC=90°,AB=AC=AD,AD交BC于点P,∠CAD=30°,AC=6,求:
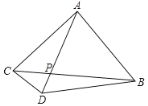
(1)∠BDC的度数,
(2)△ABD的周长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了准备科技节创意销售,宏帆初2018级某同学到批发市场购买了一些甲、乙两种型号的小元件,甲型小元件的单价是6元,乙型小元件的单价是3元,该同学的创意作品每件需要的乙型小元件的个数是甲型小元件的个数的2倍,同时,为了控制成本,该同学购买小元件的总费用不超过480元.
(1)该同学最多可购买多少个甲型小元件?
(2)在该同学购买甲型小元件最多的前提下,用所购买的甲、乙两种型号的小元件全部制作成创意作品,在制作中其他费用共花520元,销售当天,该同学在成本价(购买小元件的费用+其他费用)的基础上每件提高2a%(10<a<50)标价,但无人问津,于是该同学在标价的基础上降低a%出售,最终,在活动结束时作品全部卖完,这样,该同学在本次活动中赚了![]() a%,求a的值.
a%,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线l:y=![]() x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y=
x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y=![]() x2+bx+c经过点B,与直线l的另一个交点为C(4,n).
x2+bx+c经过点B,与直线l的另一个交点为C(4,n).
(1)求n的值和抛物线的解析式;
(2)点D在抛物线上,DE∥y轴交直线l于点E,点F在直线l上,且四边形DFEG为矩形(如图2),设点D的横坐标为t(0<t<4),矩形DFEG的周长为p,求p与t的函数关系式以及p的最大值;
(3)将△AOB绕平面内某点M旋转90°或180°,得到△A1O1B1,点A、O、B的对应点分别是点A1、O1、B1.若△A1O1B1的两个顶点恰好落在抛物线上,那么我们就称这样的点为“落点”,请直接写出“落点”的个数和旋转180°时点A1的横坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,(1)写出△ABC的各顶点坐标;
(2)画出△ABC关于y轴的对称图形△A1B1C1;
(3)写出△ABC关于x轴对称的三角形的各顶点坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
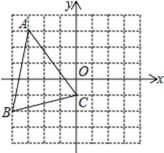
【题目】如图,在下列带有坐标系的网格中,△ABC的顶点都在边长为1的小正方形的顶点上
(1) 直接写出坐标:A__________,B__________
(2) 画出△ABC关于y轴的对称的△DEC(点D与点A对应)
(3) 用无刻度的直尺,运用全等的知识作出△ABC的高线BF(保留作图痕迹)
查看答案和解析>>
科目:初中数学 来源: 题型:
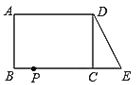
【题目】已知:如图,在长方形ABCD中,AB=4,AD=6.延长BC到点E,使CE=2,连接DE,动点P从点B出发,以每秒2个单位的速度沿BC-CD-DA向终点A运动,设点P的运动时间为![]() 秒,当
秒,当![]() 的值为_____秒时,△ABP和△DCE全等.
的值为_____秒时,△ABP和△DCE全等.
A.1B.1或3C.1或7D.3或7
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com